Number theory

Goldbach’s conjecture belongs to the field of Number theory, the branch of Mathematics which studies the properties of integer numbers. In order to understand the proofs of the results similar to the conjecture, and very likely also to prove the conjecture itself, a sound knowledge of number theory is required. But this kind of knowledge rarely is part of a mathematician’s curriculum. Indeed number theory is considered a very specialistic subject which can be taken under consideration, as an example, for some university exams selected by the student, or a doctorate, for the most enthusiastic people. But it’s not necessary going this far for undertaking a serious study of number theory. In fact, many notions require just a good knowledge of school level maths and of real analysis in one variable, so they are absolutely within the reach of a first year student of a scientifical degree course.

We started from these considerations for conceiving this site section, with the aim of allowing to as many people as possible the approach to number theory. We divided the material into different thematic paths, each with an own goal, which in most cases consists in the proof of a specifical theorem. Each path is made up of several posts, which are presented in the suggested reading order, so that each post is presented before other posts referring to it.

The source we started from is the text “An introduction to the theory of numbers” by G. H. Hardy and E. M. Write, one of the classical texts about the subject. The material we’ll cover in our posts is a heavy rework of some parts of this text: we introduced some examples, some lemmas and definitions, we highlighted the key ideas and techniques, and we added many details which are not explicit in the original text.

As an internal reference to this section of the site, we created a list of the statements and a list of the definitions and of the adopted symbols.

Map of paths for number theory

Path	Number of posts
Foundations of number theory Differently from the other paths, each of which has the goal of proving one specific theorem, the goal of this path is simply to convey a general knowledge of number theory, limited to the aspects which are mostly connected with prime numbers.	21
Bertrand’s Postulate After the Theorem about the infinity of prime numbers, perhaps the simplest theorem which states something important about the distribution of prime numbers is the so called Bertrand’s Postulate. Initially proposed as a conjecture in 1845 by the French mathematician Joseph Louis François Bertrand, the Postulate was later proved for the first time by the Russian Pafnutij L’vovič Chebyshev. It states that, for every integer number $n \gt 0$ , there exists a prime number between $n + 1$ and $2n$ (ends included), as you can see alongside in the picture.	4
Chebyshev’s Theorem (weak version) Pafnutij L’vovič Chebyshev, or Chebyshev, the mathematician who invented among the other things the “plantigrade machine” depicted alongside, is famous also for one of his theorems which constitutes a first step towards the Prime Number Theorem, and which we’ll call simply “Chebyshev’s Theorem”. There are two versions of this Theorem, called “weak” and “strong” respectively; in this path we’ll focus on the weak one.	7
Chebyshev’s Theorem (strong version) The “strong version” of Chebyshev’s Theorem (according to some authors, simply “Chebyshev’s Theorem”) constitutes, with respect to the weak one, a further step towards the Prime Number Theorem. In fact, the two Theorems are very similar, since they study the same functions, in the same way. In both cases, the functions which are studied are $\pi(x)$ , which returns the number of prime numbers less than or equal to $x$ , and $\frac{x}{\log x}$ ; the way of studying them consists in calculating their ratio, and seeing how it behaves as $x$ increases. The strong version of Chebyshev’s Theorem establishes that there are only two possibilities: either this ratio has no limit, i.e. it continues to oscillate to infinity, or, if it tends to a limit, that limit is 1.	15
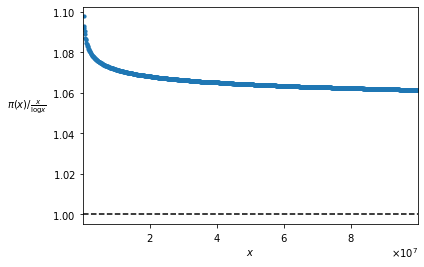
The Prime Number Theorem: the “elementary” proof The goal of this path is to prove one of the most important theorems about prime numbers, the so called Prime Number Theorem, which can be expressed by the following formula: $\pi(x) \sim \frac{x}{\log x}$ where $\pi(x)$ indicates the number of prime numbers less than or equal to $x$ . The symbol $\sim$ represents an asymptotic equivalence, the meaning of which is explained in one of our posts. However, to make things simple, we can read the formula saying that there are about $\frac{x}{\log x}$ prime numbers less than or equal to $x$ , and this estimate becomes more and more accurate as $x$ increases.	28
Chen’s Theorem The goal of this path is to prove one of the theorems most similar to Goldbach’s conjecture, Chen’s Theorem, the statement of which can be expressed as follows: Every sufficiently large even number is the sum of either two primes, or a prime and a semiprime (that is, a product of two primes). This Theorem was proved for the first time by the Chinese mathematician Chen Jingrun in 1966 (subsequently the proof was refined both by himself and by other mathematicians). The proof is based on a mathematical theory called sieve theory, developed a few years earlier but with very ancient origins, which can be traced back to the mathematician of ancient Greece Eratosthenes of Cyrene, inventor of the homonymous sieve, the first ever. Clearly, since then sieve theory has evolved a lot, but it has always remained an “elementary” theory, i.e. one not based on complex analysis.	1 (incomplete)
Complementary Material Number theory is a subject that uses many results of other mathematical subjects, first of all analysis, but also algebra and geometry. For this reason the courses about number theory are generally targeted to students who already have a solid knowledge of the other mathematical subjects at academic level, therefore to mathematically expert people. Our approach is substantially opposite, because we regard number theory as the main subject of study, and we introduce specific concepts from other subjects only when needed. So we are creating some “complementary”, i.e. supporting, posts. We’ll gather them into this path and you’ll find them inserted in the appropriate points inside the other paths.	3