Prerequirements:
In this post we’ll illustrate two properties of the divisors of natural numbers, starting from the simplest case, in which we’ll take into consideration the numbers which are the product of two distinct prime factors. Let’s take for example the number 10, which is the product of 2 and 5. So its unique non-trivial divisors, the ones different from the number itself and 1, are just 2 and 5. You can note that the number of trivial divisors (1 and 10) is equal to the number of non-trivial ones (2 and 5), and also their product is equal: 1 \cdot 10 = 2 \cdot 5. Our goal will be to generalize these two simple properties to numbers that are not necessarily the product of two different prime numbers.
Just to start, we can consider any positive integer number n instead of 10:
Two properties to be generalized
Let n be a positive integer number. If n = pq, with p and q distinct prime numbers, then its divisors are 1, p, q and n, hence:
- the non-trivial divisors are two, p and q, just like the trivial ones, that are 1 and n;
- the product of the trivial divisors is equal to the one of the non-trivial divisors: 1 \cdot n = p \cdot q.
So we can say that the example of 10 can be easily extended to all numbers which are the product of two prime factors.
Now, the next step would be attempting to generalize these two properties for broader classes of numbers. For example, we could see what happens for numbers that are the product of three distinct prime numbers, for example 30 = 2 \cdot 3 \cdot 5. The divisors of 30 are 1, 2, 3, 5, 6, 10, 15, 30. The trivial divisors, like any other number, are again two (1 and 30), but in this case there are more non-trivial divisors, and it’s easy to see that 1 \cdot 30 \neq 2 \cdot 3 \cdot 5 \cdot 6 \cdot 10 \cdot 15. So it may seem that the two properties are true only for the very particular case of numbers which are the product of two distinct prime factors, but it’s not so: there is in fact a way for generalizing them, as we’ll see in the next sections.
From now on, when we’ll talk about the “divisors” of a positive integer number, we’ll always mean the positive divisors. In fact, we’ll study the properties of \mathbb{N}, not \mathbb{Z}.
Generalization to square-free integers
Let’s recall the example of number 30. In order to understand how to generalize the two properties, it’s useful to arrange the divisors of 30 into a diagram called Hasse diagram, constructed in such a way that any two divisors d_1 and d_2 are connected by a segment if and only if d_1 \mid d_2 and there is no other divisor d_3 intermediate between them, i.e. such that d_1 \mid d_3 \mid d_2:
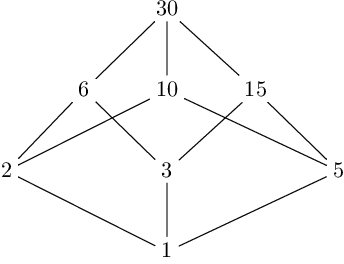
In a diagram like this, the divisors of the starting number turn out to be naturally arranged into different levels, according to the number of their prime factors. For example, in Figure 1:
- 1 is the product of zero prime factors, so it stays on the lowest level (let’s call it “level zero”);
- on the first level there are the prime factors of 30: 2, 3 and 5;
- on the second level there are the divisors of 30 which are the product of two, and only two, prime factors: 6, 10 e 15;
- 30, product of three prime factors, is the unique divisor on the third level, the highest one.
We can note that:
- The number of divisors on the odd levels is equal to the number of the ones on the even levels. They are in fact four divisors in both cases: 1, 6, 10 and 15 stay on the even levels, whereas 2, 3, 5 e 30 stay on the odd ones.
- The product of divisors on the odd levels is equal to the product of the ones on the even levels: 1 \cdot (6 \cdot 10 \cdot 15) = (2 \cdot 3 \cdot 5) \cdot 30.
The two points above are a correct way to generalize the two properties that we saw initially for numbers which are the product of two distinct prime factors. This is clear if we draw the Hasse diagram of such a number. For example, for the number 10 we have:
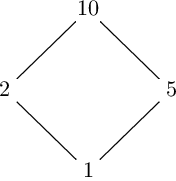
We can note that the two trivial divisors are arranged into the two even levels, whereas the two non-trivial divisors stay on the unique odd level; so, between the even and the odd levels, both the count and the product of divisors are equal.
This argument can be extended to numbers which are the product of an arbitrary number of distinct prime numbers. For example, let’s consider the number 210, that is the smallest number which is the product of four distinct prime numbers, being equal to 2 \cdot 3 \cdot 5 \cdot 7. In this case the Hasse diagram is made up of five levels:
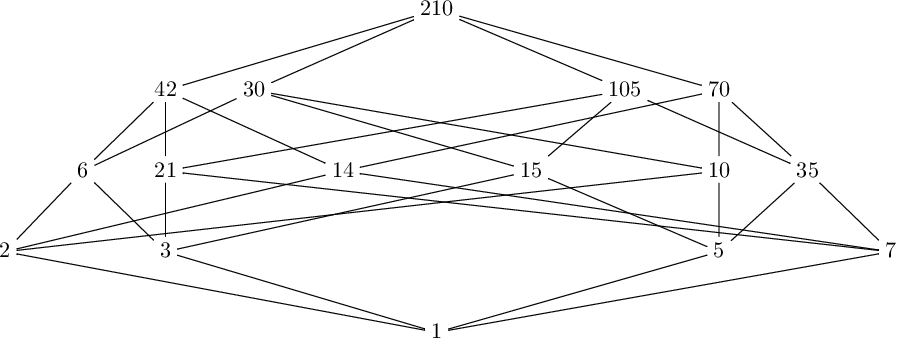
Once again, the two properties are satisfied:
- There are 1 + 6 + 1 = 8 divisors on the even levels and 4 + 4 = 8 divisors on the odd levels.
- The product of divisors on the even levels is equal to the product of divisors on the odd levels (try it by yourself!):
1 \cdot (6 \cdot 10 \cdot 14 \cdot 15 \cdot 21 \cdot 35) \cdot 210 = (2 \cdot 3 \cdot 5 \cdot 7) \cdot (30 \cdot 42 \cdot 70 \cdot 105)
In the examples seen so far, we can note that:
- if there are three levels, then there is 1 divisor on the first level, there are 2 on the second one and 1 on the third one (as it happens for the number 10);
- if there are four levels, then there is 1 divisor on the first level, there are 3 on the second one, 3 on the third one and 1 on the fourth one (as it happens for the number 30);
- if there are five levels, then there is 1 divisor on the first level, there are 4 on the second one, 6 on the third one, 4 on the fourth one and 1 on the fifth one (as it happens for the number 210).
It’s not by chance that the resulting sequences 1 2 1, 1 3 3 1 and 1 4 6 4 1 are also rows of the Pascal’s triangle, that we saw in the post Binomial estimates. In fact, it can be proved that this property about the count of divisors derives from an analogue property of binomial coefficients: for any positive integer n, the sum of the binomial coefficients of the kind \binom{n}{k}, with even k, is equal to the sum of the binomial coefficients of the same kind, with odd k.
The integer numbers which are the product of distinct prime numbers are a rather important class of numbers, that now it’s worth to analyze better. There is in fact an equivalent concept, the one of square-free integer:
Square-free integer
An integer number is called square-free if it’s not divisible by any square number greater than 1.
Characterization of square-free integers
An integer number is square-free if and only if in its factorization there are only distinct prime factors.
We’ll prove the equivalent statement obtained by negation of both members: “An integer number is not square-free if and only if in its factorization there is at least one repeated prime factor”.
The proof is immediate:
- If n is not square-free, then there exists a square number a^2 \gt 1 such that a^2 \mid n. Then each prime factor of a, appearing at least twice in the factorization of a^2, will appear at least twice also in the factorization of n, so the latter cannot contain only distinct prime factors.
- If in the factorization of n there is a repeated prime factor p, then p^2 \mid n, so n is not square-free.
So, by Property N.7, hereinafter we’ll be able to say indifferently that an integer number is “product of distinct prime factors” or it’s “square-free”.
Summarizing, we saw by several examples that the two properties we are studying – that hereinafter we’ll also call “count property” and “product property” – are both true for square-free integers with an increasing number of prime factors, starting from 2. For prime numbers, that may be considered as the product of only one prime factor, only the first property is true. For example, the Hasse diagram of the number 3 is the following:
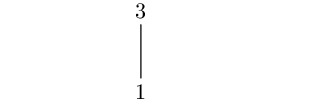
There is one divisor on the unique even level and another one on the unique odd level, so the count property is satisfied. However, the products of divisors on each level are different, because both are products of a single number, so they coincide with the number itself, but the two numbers are different.
Instead, if the prime factors, all distinct, are at least two, they haven’t to be necessarily consecutive. For example, we invite you to check that the two properties are satisfied also for the number 330 = 2 \cdot 3 \cdot 5 \cdot 11, even if its prime divisors are not all primes up to 11, because they lack 7.
The problems begin when we consider numbers in the factorization of which there is a prime repeated more than once (or, equivalently, a prime number raised to an exponent greater than 1). For example, if rather than 30 = 2 \cdot 3 \cdot 5 we considered the number 60 = 2 \cdot 2 \cdot 3 \cdot 5, where the 2 appears twice, the number of divisors would be as expected, but we could not say the same thing about the product. In fact, the Hasse diagram of the divisors of 60 is the following:

There are 1 + 4 + 1 = 6 divisors on the even levels and 3 + 3 = 6 on the odd levels, so the count property is satisfied; however the product of factors on the even levels is 1 \cdot 4 \cdot 6 \cdot 10 \cdot 60 = 14,400, whereas the product of those ones on the odd levels is 2 \cdot 3 \cdot 5 \cdot 12 \cdot 20 \cdot 30 = 216,000.
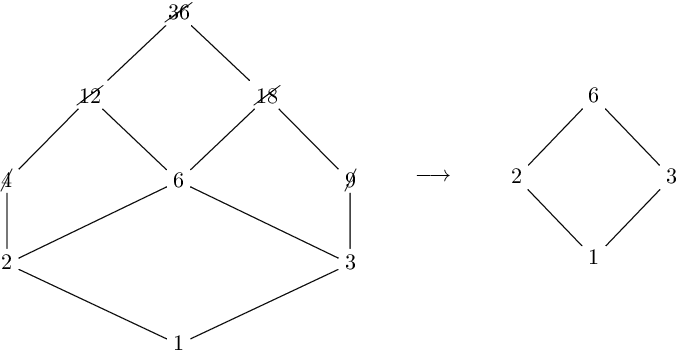
We could think that the problem is that the repetition of the 2 generates an imbalance between the divisors, because not all of them appear in the factorization the same number of times, but it’s not so. In fact, if we consider the number 2 \cdot 2 \cdot 3 \cdot 3 = 36, where both the prime factors are repeated twice, it will be even worse, because not only the product property will not be satisfied, but also the count property:
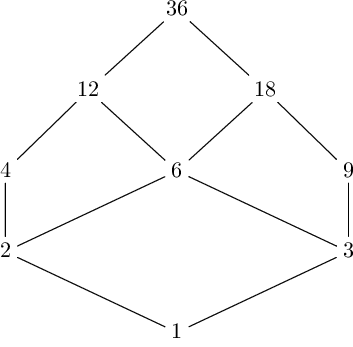
In fact, in this case there are 1 + 3 + 1 = 5 divisors on the even levels and 2 + 2 = 4 on the odd levels, and their products are different: 1 \cdot 4 \cdot 6 \cdot 9 \cdot 36 \neq 2 \cdot 3 \cdot 12 \cdot 18.
This is a good question: in fact it’s reasonable to think that a different way to arrange the divisors into levels exists, in order to balance calculations for numbers like 60 o 36. We don’t know a general answer to this question, but we can say that it’s not so simple.
For example, a meaningful choice may be considering each level l as the set of divisors in the factorization of which there are not l prime factors, but l distinct prime factors, so ignoring the repetitions of the same prime factor.
If we try to split the divisors of 60 this way, we’ll have that:
- 1 is always the only product of 0 prime factors, so it will remain the only divisor of level 0
- 2, 3, e 5 are the product of a single prime factor, so, like before, they will belong to level 1; but also the 4 will belong to level 1, because in its factorization there is only the prime factor 2: ignoring the repetition, there is again a single prime factor.
- 6, 10 e 15 are the product of two distinct prime factors, so, like before, they will belong to level 2; but also 12 e 20 will belong to level 2, because in their factorization there are two distinct prime factors too: 2 and 3 in the case of 12; 2 and 5 in the case of 20.
- Both in the factorization of 30 and in the one of 60 there are three distinct prime factors: 2, 3 e 5; so both numbers will belong to level 3.
Rearranging the Hasse diagram of 60 this way, we’ll obtain the following picture:
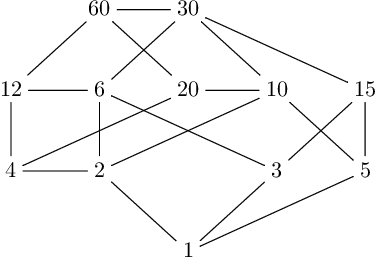
Now the properties are satisfied: the count of divisors is 1 + 5 = 6 for the even levels and 4 + 2 = 6 for the odd levels; moreover the product of the divisors on the even levels is equal to the product of those ones on the odd levels: 1 \cdot 12 \cdot 6 \cdot 20 \cdot 10 \cdot 15 = 216,000 = 4 \cdot 2 \cdot 3 \cdot 5 \cdot 60 \cdot 30. So it may seem that we have found the right manner to split the divisors of a positive integer number into even levels and odd levels. But this method does not work with all numbers. For example, for the number 46 we would obtain the following diagram, that satisfies neither of the two properties:
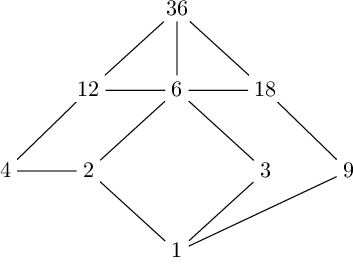
As you can easily check, the count of divisors is 4 for the even levels and 5 for the odd ones, and the product of divisors on the even levels is different from the product of those ones on the odd levels.
So the question: “is there a more general way to rearrange the divisors into levels, such to satisfy the two properties we are studying, also in the presence of repeated prime factors?” remains open. However we can say for sure that, if such a method existed, it would not be valid for all numbers. In fact, a necessary condition for the existence of such a method is that the product of all the divisors of n is a square number. In fact, indicating by E_n the product of divisors on the even levels, by O_n the product of those ones on the odd levels, and by A_n the product of all the divisors of n, since by hypothesis E_n = O_n, we must have that A_n = E_n \cdot O_n = E_n \cdot E_n = E_n^2, hence A_n must be a square number. But this is not true for example for 36, because the product of its divisors, 1 \cdot 4 \cdot 2 \cdot 3 \cdot 9 \cdot 12 \cdot 6 \cdot 18 \cdot 36, is not a square number.
Generalization to any integer number greater than one
Given the difficulty to generalize the two properties to any positive integer number, we can resort to a simple artifice in order to bring us back to the case of square-free numbers: it’s enough to remove, from the Hasse diagram, all the divisors which are not square-free (equivalently, by Property N.7, in the factorization of which there is at least one prime repeated more than once). For example, starting from the Hasse diagram of 60, we have to remove the divisors 4, 12, 20 and 60, because in their factorization the 2 is repeated twice: 4 = 2 \cdot 2, 12 = 2 \cdot 2 \cdot 3, 20 = 2 \cdot 2 \cdot 5 and 60 = 2 \cdot 2 \cdot 3 \cdot 5. Doing so, we’ll obtain the Hasse diagram of 30, which is a square-free integer, being the product of the distinct prime factors of 60:
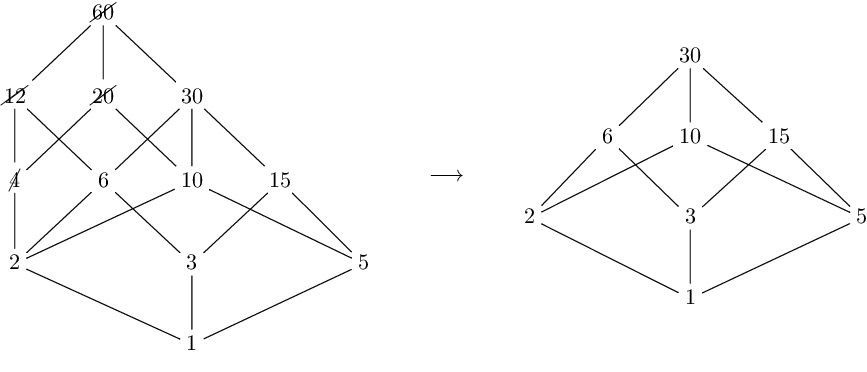
Similarly, starting from the Hasse diagram of 36 and doing the same operation, we’ll obtain the Hasse diagram of 6, which is square-free being the product of the distinct prime factors of 36:
If instead the initial number is the power of a prime number with an exponent greater than 1, like 81 = 3^4, removing the divisors which are not square-free means removing all powers with an exponent greater than 1, so, in the case of 81, we’ll end up with an Hasse diagram containing just 1 and 3, that is the Hasse diagram of 3:
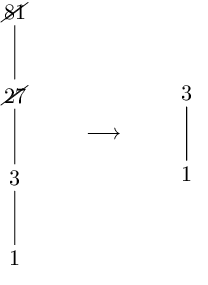
We saw that in this case only the count property is satisfied, not the product one. So, generally we can say that, after removing the divisors which are not square-free (i.e. with repeated prime factors), the product property is satisfied when in the factorization of the initial number there are at least two distinct prime numbers; instead, the count property is satisfied also when in the factorization there is only one prime number, optionally repeated more than once.
The number 1 is a degenerate case, because it may be considered as the product of 0 prime factors, but we are interested to numbers which have at least one prime factor, optionally repeated. We’ll choose to neglect the case of the number 1 partially for the above reason, and also because the properties are not satisfied according to the general rule. In fact the count property is not satisfied (the unique divisor 1 is the product of an even number (0) of prime factors, and there aren’t any divisors which are the product of an odd number of prime factors) whereas the product property is satisfied (1 is the product of the set \{1\} of the divisors which are the product of an even number of distinct prime factors, but it’s also the product of the empty set of the divisors which are the product of an odd number of distinct prime factors).
So, we can state the count property and the product property as follows:
A property about the count of divisors of an integer greater than 1
Let n \gt 1 be an integer number. Let E_n and O_n be the following sets:
Then
We may bring back this proof to a similar property of sets: given any set of n elements, the number of subsets with an even number of elements is equal to the number of subsets with an odd number of elements. If this property is assumed to be already known, it would be simple to prove Property N.8. However, we’ll do the proof from scratch, with the same type of argument which can be used for the case of sets, because later, with a small modification, we’ll able to prove the product property too.
Let’s call k the number of distinct prime factors of n and let’s proceed by induction on k. The base case is k = 1, that happens when in the factorization of n there is only one distinct prime factor, which we’ll call q, i.e. when n is a power of q with a positive exponent. For such n, the only square-free divisors are 1 (product of 0 primes) and q (product of a single prime factor), because any other divisor of n would be a power of q with an exponent greater than 1, the factorization of which would contain the prime q repeated more than once. So E_n = \{1\} and O_n = \{q\}, hence the base case is satisfied, being |E_n| = |O_n| = 1.
Now let’s suppose that the property is satisfied for k - 1 and let’s prove it for k, with k \geq 2.
In order to do that, we have to ask ourselves what are the elements of E_n and O_n for a number n which has k distinct prime factors, somehow bringing the answer back to the case of a number which has k - 1 distinct prime factors, in order to use the induction hypothesis. One way to to that consists in eliminating from the factorization of n any one of its prime factors, which we’ll call p, along with its possible repetitions. Thus we’ll obtain a new number n^{\prime}, in the factorization of which there will be k - 1 distinct prime factors, so we’ll be able to apply the induction hypothesis to this number, obtaining that |E_{n^{\prime}}| = |O_{n^{\prime}}|. But how are the sets E_n and O_n related to the sets E_{n^{\prime}} and O_{n^{\prime}}?
Let’s start from E_n. First of all, let’s note that a divisor d of n belonging to E_n may contain or not contain p in its factorization:
- If the factorization of d does not contain p, then d is also a divisor of n^{\prime}, because the latter has the same prime factors as n, except only p and its possible repetitions. So d \in E_{n^{\prime}}.
- If the factorization of d contains p (and in this case, by the definition of E_n and by Property N.7, it contains p just once), we can divide d by p, obtaining the number \frac{d}{p} that will be the product of distinct prime factors, all different from p. Then, like before, being n^{\prime} the product of all the prime factors of n different from p, surely \frac{d}{p} \mid n^{\prime}. In addition, \frac{d}{p} is the product of an odd number of distinct prime factors (because they were initially even and we eliminated p), hence, again by Property N.7, \frac{d}{p} \in O_{n^{\prime}}. Equivalently, we can say that d = p \cdot a, for some a \in O_{n^{\prime}}, or also that d \in p \cdot O_{n^{\prime}}, where the set p \cdot O_{n^{\prime}} has been obtained by O_{n^{\prime}} by multiplicating all its elements by p, i.e. p \cdot O_{n^{\prime}} := \{p \cdot a | a \in O_{n^{\prime}}\}.
Considering these two possibilities together, we’ll have that d \in E_{n^{\prime}} or d \in p \cdot O_{n^{\prime}}, so d \in E_{n^{\prime}} \cup p \cdot O_{n^{\prime}}. But this is true for all d \in E_n, hence
- n^{\prime} = 3 \cdot 5
- E_n = \{1,\ 2 \cdot 3,\ 2 \cdot 5,\ 3 \cdot 5\} (in particular 2 \cdot 2 \notin E_n and 2 \cdot 2 \cdot 3 \cdot 5 \notin E_n because these divisors of n are not square-free)
- E_{n^{\prime}} = \{1,\ 3 \cdot 5\}
- O_{n^{\prime}} = \{3,\ 5\}
- 2 \cdot O_{n^{\prime}} = \{2 \cdot 3,\ 2 \cdot 5\}
- 1 is the product of 0 prime factors (different from p) \Rightarrow 1 \in E_{n^{\prime}}
- 2 \cdot 3 is the product of 2 distinct prime factors, among which p \Rightarrow 2 \cdot 3 \in 2 \cdot O_{n^{\prime}}
- 2 \cdot 5 is the product of 2 distinct prime factors, among which p \Rightarrow 2 \cdot 5 \in 2 \cdot O_{n^{\prime}}
- 3 \cdot 5 is the product of 2 distinct prime factors, different from p \Rightarrow 2 \cdot 3 \in E_{n^{\prime}}
The previous argument can be repeated by looking at relationship (1) in the opposite direction. In fact, starting from a divisor d^{\prime} of n^{\prime}, we’ll have two possibilities:
- If d^{\prime} \in E_{n^{\prime}}, first of all d^{\prime} is the product of an even number of prime factors; moreover d^{\prime} is a divisor of n^{\prime}, which in turn is a divisor of n, hence d^{\prime} is also a divisor of n; considering both things, d^{\prime} \in E_n.
- If d^{\prime} \in p \cdot O_{n^{\prime}}, d^{\prime} is the product of p by an odd number of distinct prime factors different from p, so it’s the product of an even number of distinct prime factors. Moreover it’s a divisor of n, because \frac{n^{\prime}}{p} \in O_{n^{\prime}} \Rightarrow \frac{n^{\prime}}{p} \mid n^{\prime}, from which n^{\prime} \mid (p \cdot n^{\prime}) \mid n, so n^{\prime} \mid n. Summarizing, being n^{\prime} a divisor of n and the product of an even number of distinct prime factors, taking into account Property N.7 again, also in this case d^{\prime} \in E_n.
So we have obtained the converse of (1), that is
Combining (1) and (2), we’ll obtain the following fundamental relationship:
We can repeat the same argument for O_n, obtaining finally:
Now we have to compute the cardinality of E_n and O_n starting from formulas (3) and (4). Before doing that, we have to remark some things:
- The sets of the union are disjoint, because the elements of the right set are all multiples of p, whereas the elements of the left set cannot be such, because they are divisors of n^{\prime}, and p does not appear in the factorization of n^{\prime}.
- The sets p \cdot O_{n^{\prime}} and p \cdot E_{n^{\prime}} have respectively the same cardinality as O_{n^{\prime}} and E_{n^{\prime}}. In fact, looking for example at the sets p \cdot O_{n^{\prime}} and O_{n^{\prime}}, the first one is obtained by multiplicating by p all the elements of the second one; doing so, starting from distinct element of O_{n^{\prime}}, distinct elements of p \cdot O_{n^{\prime}} are obtained (in other words, the multiplication by p is an injective function), hence |p \cdot O_{n^{\prime}}| = |O_{n^{\prime}}|.
- By induction hypothesis, |E_{n^{\prime}}| = |O_{n^{\prime}}|, so we can indicate both with a constant C.
By combining these remarks, from formula (3) we’ll obtain that:
While from (4) we’ll obtain:
So |E_n| = |O_n|, that is what we wanted to prove.
A property about the product of divisors of a positive integer number with at least two distinct prime factors
Let n be a positive integer number with at least two distinct prime factors. Let E_n and O_n be the sets defined in Property N.8. Then
You have to pay attention to the difference between the expressions “with at least two distinct prime factors” and “product of at least two prime factors”. In the first case, which is the hypothesis of Property N.9, we mean that n may have repeated primes in its factorization, but al least two of them must be distinct: for example 12 = 2 \cdot 2 \cdot 3 is ok but 4 = 2 \cdot 2 is not. In the second case, we mean that in the factorization of n there are only distinct prime factors, and the number of them is at least two. So the second expression is a particular case of the first one, and the two concepts must not be confused with each other. For this reason we defined the elements of the sets E_n and O_n as “square-free”, thus avoiding the abuse of the expression “distinct prime factors”.
As we said before, the proof of this property is just a small modification of the one of the previous property. We’ll proceed again by induction on k, the number of distinct prime factors of n, but in this case the base step is k = 2.
If k = 2, in the factorization of n there are exactly two distinct prime factors. Then the divisors contained in the set E_n, by definition, can be the product of 0 or 2 distinct prime factors, because they are the only even numbers less than or equal to k = 2. The only product of 0 prime factors is 1, so 1 \in E_n and all the other elements of E_n are the products of two distinct prime factors. But n has only two distinct prime factors, which we can call p and q, so the only possible product of this kind is pq (we have to neglect by definition possible divisors which are not square-free, like p^2). Then E_n = \{1, pq\}. On the other hand, concerning O_n, the only possible elements by definition are the divisors which are the product of a single prime number, because 1 is the only odd number less than or equal to k = 2. But the product of a single prime number is the prime number itself, so the elements of O_n are simply the prime factors of n, that is O_n = \{p, q\}. So the base case is satisfied, being \prod_{a \in E_n} a = 1 \cdot pq = p \cdot q and \prod_{b \in O_n} b = p \cdot q.
Now let’s suppose that the property is satisfied for k - 1 and let’s prove it for k, with k \geq 3.
Let’s start from equations (3) and (4) we have seen inside the proof of the previous property:
By (3), since the union is disjoint, the product of the elements of E_n is equal to the product of the elements of E_{n^{\prime}} multiplicated by the product of those ones of the set p \cdot O_{n^{\prime}}. Moreover, being p \cdot O_{n^{\prime}} = \{p d_1^{\prime}, p d_2^{\prime}, \ldots, p d_{|O_n^{\prime}|}^{\prime}\}, where d_1^{\prime}, d_2^{\prime}, \ldots, d_{|O_n^{\prime}|}^{\prime} are the elements of O_{n^{\prime}}, by gathering on the left all the factors p we’ll have that the product of the elements of p \cdot O_{n^{\prime}} is equal to p^{|O_n^{\prime}|} multiplicated by the product of the elements of O_{n^{\prime}}:
But, by the induction hypothesis, the product of the elements of E_{n^{\prime}} is equal to the product of the elements of O_{n^{\prime}}, so we can indicate both with a constant P:
Starting from formula (4), we can argument similarly, obtaining:
Hence:
Now, comparing formulas (5) and (6), and noting that, by Property N.8, |O_n^{\prime}| = |E_n^{\prime}|, we’ll obtain the equality between the product of the elements of E_n and the one of the elements of O_n:
In the next post we’ll see that Properties N.8 and N.9 justify the definition of an important function of number theory: the Möbius function.