When studying number theory, you’ll soon realize that some familiarity with certain formalisms is required. In particular, some kinds of summations are so common that it’s worth treating them separately, before applying them in various contexts. This is what we’ll do in this post, which can be skipped at first, but it will be a reference for the next posts.
Some formalisms about summations
We know that, when many numbers have to be summed up, the sum can be written in a compact way by using the summation symbol. For example, the sum of squares of the integers from 1 to n, where n \geq 1 is an integer, can be written as follows:
or, equivalently:
or also:
All the previous notations are equivalent to the following explicit one:
Though this kind of notation is often more understandable than the equivalent summations, many times summations turn out to be more practical when algebraic calculations are involved, especially in proofs.
Generally the terms of a summation, that are the addends of the sum, can be the result of any function f of the variable i, which is called index (or variable) of the summation:
Computing this summation means to compute f(i) for all i = 1, \ldots, n, and summing up all the obtained values: a corresponding explicit notation would be f(1) + \ldots + f(n). It’s also possible, in the latter notation, to explicit more terms before the dots, for example f(1) + f(2) + f(3) + \ldots + f(n); however, whatever the number of explicited terms is, n is supposed to be at least equal to the index of the first term, in this case 1, hence for example if n = 2 the notation f(1) + f(2) + f(3) + \ldots + f(n) reduces to f(1) + f(2): the term f(3) is not really present but it only helps to make clear how the summation would behave for greater values of n.
In many summations used in number theory, the index does not vary within all the integers between 1 and n, but only within the divisors of n, so usually it’s denoted with the variable d:
This means calculating f(d) only for the positive integers d that divide n, and summing up the obtained values:
Summations extended to the divisors of a positive integer
Let n \in \mathbb{N}^{\star}. We define the following symbol:
where for “divisors”, as usual, we mean the positive divisors.
In order to clarify the difference between summations (1) and (2), let’s see an example. For n = 6, summation (1) becomes:
while summation (2) becomes:
The next step is to consider double summations, which consist in two nested summations, an inner summation and an outer one, where each summation has a different variable varying within an own set of values. There are several types of double summations, but we are specially interested in the ones where the variable of the inner summation is bounded by the one of the outer summation, like in the following case:
Computing this summation means to let i vary between 1 and n, to let j vary between 1 and i for each value of i, to compute the value of f(i, j) for each couple (i, j) so obtained, and finally to sum up everything.
Considering only the divisors of n, we’ll obtain the following summation, analogous to (1′):
Computing this summation means to let d vary between the divisors of n, to let d^{\prime} vary within the set of divisors of d for each value of d, to compute for each couple (d, d^{\prime}) the value of f(d, d^{\prime}), and finally to sum up everything.
For n = 6, summation (1′) becomes:
while summation (2′) becomes:
There are also some double summations which at first glance may seem single summations, because the summation symbol (\Sigma) appears just once, but it’s more correct to consider them double summations, because indexes are still two. An example is the following:
Summations extended to couple of variables with constant product
Let n be a positive integer. We define the following symbol:
Figure 1 helps to understand what means to consider all the couples of indexes a and b having constant product (we chose n = 10).
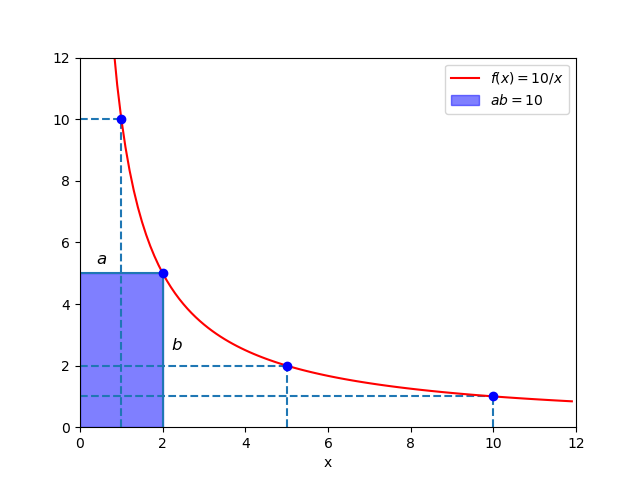
If we replace the equality symbol with the divisibility simbol, we’ll obtain another kind of summation which is rather recurring in number theory:
Summations extended to couples of variables the product of which divides a constant
Let n be a positive integer. We define the following symbol:
This kind of summation is a bit more difficult to visualize, but we’ll do it in a moment, after we’ll have seen a property which lets rewrite the summation in a different way.
Finally there is a third variation of this kind of summation, with the \leq sign:
Summations extended to couples of variables the product of which is less than or equal to a constant
Let n be a positive integer. We define the following symbol:
Figure 2 helps to understand what means to consider all the couples of indexes a and b the product of which is less than or equal to a constant (like in Figure 1, we chose n = 10).
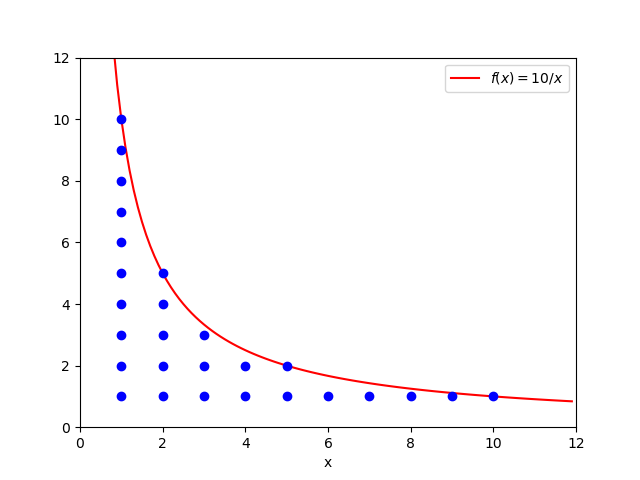
The definitions given so far can be extended to the case of productions. They are a compact way for denoting the product of a certain number of factors, instead of the sum of a certain number of addends, and they are denoted by the uppercase Greek Pi symbol (\Pi). For example, (1) in the case of productions becomes:
which means:
that is the product of all the factors of the kind f(i), for i that varies between 1 and n.
In order to extend our definitions to the case of productions, it’s sufficient to replace the summation symbol (\Sigma) with the production one (\Pi) and the sum operation with the product one. For example, recalling Definition N.20 we can define:
The new definitions that would be obtained this way will not be necessary in the future, so we’ll omit them in this post, but for completeness we have defined also the production symbols, along with the summation ones, in the page Number theory definitions and symbols.
In order to conclude this list of symbols, we’ll introduce a convention which is very common in number theory: when the index of a summation starts with 1, this value is often implied:
Summations starting from 1
Let x be a positive integer. We define the following symbol:
In the next sections we’ll see some commonly used properties regarding the types of summations which have been defined in this section.
Summations where the product of indexes is equal to a constant
There is a connection between the summations where the product of indexes is equal to a constant and those ones extended to the divisors of a number:
Equivalent form for summations with d and \frac{n}{d}
Let n be a positive integer number. Let f be any function defined on \mathbb{N}^{\star} \times \mathbb{N}^{\star} (the codomain does not matter(*)). Then:
(*) To be precise, it’s necessary that the operations of sum and product are defined on the codomain, and they must be commutative. However in this context there is no problem at all, because this is true for the numerical sets we are interested in, that are \mathbb{N}, \mathbb{Z} and \mathbb{R}.
The proof technique that we’ll use for all the statements of this post consists in showing that all the terms of the right summation appear also in the left summation, and vice versa.
Let’s consider a term of the right summation, that is f\left(d, \frac{n}{d}\right), for some fixed d, divisor of n. Setting a := d and b := \frac{n}{d}, we’ll have that a and b are two positive integers such that ab = n, so the left summation will contain the term f(a,b). But f(a, b) = f\left(d, \frac{n}{d}\right), so f(a,b) is just the term we had chosen on the right. Since this argument can be repeated for each value of the variable d of the right summation, we’ll have that all the terms of the right summation will appear also in the left summation.
Now let’s consider a term of the left summation, i.e. f(a, b), where a and b are two positive integers such that ab = n. We can note that, in the latter equality, a is a divisor of n and b = \frac{n}{a}. Then, setting d := a, we’ll have that f(a, b) = f\left(a, \frac{n}{a}\right) = f\left(d, \frac{n}{d}\right), hence the term f(a, b) we had chosen in the left summation will appear also in the right one. Since this argument can be repeated for each term of the left summation, we’ll have that all the terms of the left summation appear also in the right one. This completes the proof.
Summations where the product of indexes is less than or equal to a constant
The summations where the product of indexes is less than or equal to a constant can be reduced to the ones where the product of indexes is equal to a constant:
Equivalent form for summations where the product of indexes is less than or equal to a constant
Let n be a positive integer number. Let f be any function defined on \mathbb{N}^{\star} \times \mathbb{N}^{\star} (the codomain does not matter(*)). Then:
(*) The same observations made about Property N.14 are also valid now
The proof of this Property begins from the observation that both summations consider the values of f(a, b) for all the couples of positive integers a and b the product of which is less than or equal to n, but while the first summation does not specify the order in which terms are summed up, the second sorts them with respect to the product ab, which is named k.
In fact, let’s consider one term f(a, b) of the left summation, i.e. such that ab \leq n. Setting k := ab, we’ll find k within the summation \sum_{k \leq n} and, since ab = k, we’ll find the term f(a, b) also in the right summation. Conversely, let’s consider a term f(a, b) of the right summation: we’ll have that ab = k and k \leq n, hence ab \leq n, so the term f(a, b) that we had chosen is present also in the left summation. So the two summations have the same terms overall, so their values coincide.
There is also another way in which summations of this kind can be rewritten:
Second equivalent form for summations where the product of indexes is less than or equal to a constant
Let n be a positive integer number. Let f be any function defined on \mathbb{N}^{\star} \times \mathbb{N}^{\star} (the codomain does not matter(*)). Then:
(*) The same observations made about Property N.14 are also valid now.
Let (a, b) be a couple of indexes of the right double summation. Since \left\lfloor \frac{n}{a} \right\rfloor is the quotient of the division of n by a, we can indicate it with q and set n := qa + r, where r is the remainder of the same division. Then b \leq \left\lfloor \frac{n}{a} \right\rfloor \Rightarrow b \leq q \Rightarrow ab \leq aq \leq n, so the couple of indexes (a, b) will occur also in the left summation.
Conversely, let (a, b) be a couple of indexes of the left summation, i.e. such that ab \leq n. Then a \leq \frac{n}{b} \leq n; moreover b \leq \frac{n}{a} but, since it’s an integer, we must have that b \leq \left \lfloor \frac{n}{a} \right \rfloor. So the couple of indexes (a, b) occurs also in the right summation.
So, the two summations have exactly the same values for the indexes a and b and then, since they also have the same general term f(a, b), they are equal.
Summations where the product of indexes divides a constant
The summations where the products of indexes divides a constant can be reduced to those ones where a single index divides a variable:
First equivalent form for summations where the product of indexes divides a constant
Let n be a positive integer number. Let f be any function defined on \mathbb{N}^{\star} \times \mathbb{N}^{\star} (the codomain does not matter(*)). Then:
(*) The same observations made about Property N.14 are also valid now
Let (a, b) be a couple of indexes of the summation \sum_{ab \mid n} f(a, b), i.e. such that ab \mid n. In order that these indexes appear also in the right summation, the following conditions must be satisfied, for some integer k:
- ak = n
- b \mid k
Of course k must be equal to \frac{n}{a}, by the first equation. We can note that k := \frac{n}{a} is an integer number, because ab \mid n \Rightarrow a \mid n. Let’s see if this value of k satisfies also the second equation. Starting from the hypothesis that ab \mid n, we’ll have that there exists an integer c such that n = abc \Rightarrow \frac{n}{a} = bc \Rightarrow k = bc \Rightarrow b \mid k. So the second equation is satisfied too, so the couple of indexes (a, b) taken from the left summation occurs also in the right one. We can note that, in the right summation, the number k is not really an index of the summation, because it’s not used in the term f(a, b), but it’s only an auxiliary variable which lets define the values of a and b.
Conversely, let (a, b) be a couple of indexes of the summation \sum_{ak = n} \sum_{b \mid k} f(a, b). So there exists an integer k such that ak = n and b \mid k. In order that the indexes a and b occur also in the left summation, we must have that ab \mid n. Considering the hypothesis ak = n and b \mid k, we’ll have that k = bc for some integer c, and so n = ak = abc, hence ab \mid n. So the couple of indexes which we had chosen will occur also in the left summation.
So, the two summations have exactly the same values for the indexes a and b and then, since they also have the same general term f(a, b), they are equal.
Property N.22 is depicted into Figure 3.
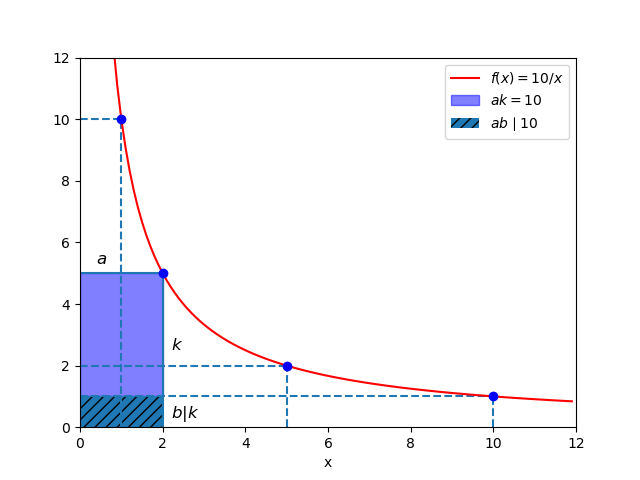
It’s also possible to use the divisibility symbol for both indexes:
Second equivalent form for summations where the product of indexes divides a constant
Let n be a positive integer number. Let f be any function defined on \mathbb{N}^{\star} \times \mathbb{N}^{\star} (the codomain does not matter(*)). Then:
(*) The same observations made about Property N.14 are also valid now
The proof of this Property can be obtained from the one of Property N.20, replacing the less than or equal symbol (\leq) with the divisibility symbol (\mid) and taking into account that, since b is a divisor of n, \frac{n}{b} = \left\lfloor \frac{n}{b} \right\rfloor. Anyway, for better clarity, we’ll write down the specific proof of this Property.
Let (a, b) be a couple of indexes of the summation \sum_{b \mid n} \sum_{a \mid \frac{n}{b}} f(a, b). We’ll have that a \mid \frac{n}{b} \Rightarrow ab \mid n, so the couple of indexes (a, b) will occur also in the summation \sum_{ab \mid n} f(a, b).
VConversely, let (a, b) be a couple of indexes of the latter summation, i.e. such that ab \mid n. Then also b \mid n; moreover ab \mid n \Rightarrow \exists c \text{ such that } n = abc \Rightarrow \frac{n}{b} = \frac{abc}{b} = ac \Rightarrow a \mid \frac{n}{b}. So the couple of indexes (a, b) occurs also in the summation \sum_{b \mid n} \sum_{a \mid \frac{n}{b}} f(a, b).
So, the two summations have exactly the same values for the indexes a and b and then, since they also have the same general term f(a, b), they are equal.
Let’s evaluate the summations \sum_{ak = n} \sum_{b \mid k} f(a, b) and \sum_{b \mid n} \sum_{a \mid \frac{n}{b}} f(a, b) separately, for n = 12:
Comparing the obtained results, we can see that they are equal up to the order of addends, so the final sum is the same. In particular, there are all and only the terms of the type f(a, b) such that ab \mid 12, so both the summations coincide with the summation \sum_{ab \mid 12} f(a, b).
There is also a third way in which the summations of this kind can be rewritten:
Third equivalent form for summations where the product of indexes divides a constant
Let n be a positive integer number. Let f be any function defined on \mathbb{N}^{\star} \times \mathbb{N}^{\star} (the codomain does not matter(*)). Then:
(*) The same observations made about Property N.14 are also valid now
We’ll follow the same principle of the proofs of the previous Properties: in order to show that the two summations are equal, we have to check that each term which appears on the right appears also on the left, and vice versa.
Let’s consider one term of the left summation. It’s given by f(a, b), where a and b are two positive integers such that ab \mid n. Let’s see if this term appears also in the right summation. If yes, there would exist two positive integers d and d^{\prime} such that:
- d \mid n
- d^{\prime} \mid d
- d^{\prime} = a
- \frac{d}{d^{\prime}} = b
But such integers exist, because, as we can obtain from the last two equations, it’s sufficient to set:
In fact, these values of d and d^{\prime} satisfy also the first two equations, since by hypothesis ab \mid n. So the mapping (a) lets associate to each possible couple of values for the variables (a, b) in the left summation, a couple of values for the variables (d, d^{\prime}) which generate the same term in the right summation.
Thus we have proved that all the terms of the left summation appear in the right one; now we have to prove the converse. So, let’s consider one term of the right summation. It will be of the kind f\left(d^{\prime}, \frac{d}{d^{\prime}}\right), where d is a divisor of n and d^{\prime} is a divisor of d. Will we find this term also in the left summation? If yes, there should exist two positive integers a and b such that:
- ab \mid n
- a = d^{\prime}
- b = \frac{d}{d^{\prime}}
The values of a and b are given by the last two equations:
But these values satisfy also the first equation, since ab = d^{\prime} \frac{d}{d^{\prime}} = d \mid n.
So, the mapping (b) lets associate to each possible couple of values for the variables (d, d^{\prime}) of the right summation, a couple of values for the variables (a, b) which generate the same term in the left summation. This ensures that all the terms of the left summation appear also in the right one, and it completes the proof.
Let’s see an example with n = 12:
At the end we have obtained the sum of all the possible terms of the kind f(a, b), where ab is a divisor of n, hence the initial summation reduces to the following form: