Prerequirements:
- The Prime Number Theorem: history and statement
- Chebyshev’s Theorem (strong version)
- From real numbers to integer numbers
- Chebyshev’s Theorem (weak version)
In the previous post we saw that the only difference between the statement of the strong version of Chebyshev’s Theorem and the one of the Prime Number Theorem, is that the first theorem does not assert the existence of the limit
whereas the second one does. In fact, it’s not by chance that the general idea of the Prime Number Theorem proof consists in starting from the proof of Chebyshev’s Theorem (strong version), reusing the main parts of it in order to prove the remaining part of the statement, that is the existence of the limit (1). So we can see Chebyshev’s Theorem as an intermediate leg, a source of inspiration for achieving the Prime Number Theorem.
Reading again the post about the strong version of Chebyshev’s Theorem, we can see that the key passage — the one that let us say that the limit (1), if it exists, is 1 — is the following equation:
This will be our starting point. Our goal will be to understand something more about the function \psi (and about its simple extension \overline{\psi}), finally proving that:
In fact, if we prove this, we can get to the Prime Number Theorem in a single passage, given that, by Corollary of Theorem N.5 (Asimptotic equivalence between \pi(x) and \frac{\psi(x)}{\log x}), \pi(x) \sim \frac{\psi(x)}{\log x}, and so by transitivity we’ll have:
Now that the starting point and the goal are clear, we can actually start with the proof. It will be long and complex, but we’ll try to highlight the key passages, for avoiding to lose the thread. Now we have to remember formulas (2) e (3′) that are respectively the initial one and the final one; in the next posts we’ll see what other important formulas there are in the middle.
The first passage of the proof, which is the subject of this post, is a technical artifice: it consists in rewriting (2) in a simpler form, eliminating the square at the denominator and the logarithm. By appropriate passages we can get to the following form:
Starting from formula (2), first of all we can note that \log x = \int_1^x \frac{1}{t} dt; in fact, calculating this integral, we’ll obtain that \int_1^x \frac{1}{t} dt = [\log t]_1^x = \log x - \log 1 = \log x - 0 = \log x. By rewriting the logarithm this way and using the properties of the algebraic sum of integrals, we’ll obtain:
Now, in order to eliminate the factor \frac{1}{t} inside the integral, it’s possible to use the substitution t := e^u, hence dt = e^u du. As a result of this substitution, the integral ends change because, if t = 1, then e^u = 1, and so u = 0, that becomes the new lower end; similarly, if t = x then e^u = x and so u = \log x, that becomes the new upper end. With these substitutions, we can obtain formula (4):
The integrand function has a very simple structure, being expressible as the composition of the function \frac{\overline{\psi}(t) - t}{t}, with the exponential function. From now on, we’ll call the integrand function V and its first component function W:
Functions W and V
We define the following functions W: [1, +\infty) \rightarrow \mathbb{R} and V: \mathbb{R}_{+} \rightarrow \mathbb{R}:
From Definition N.13 it follows immediately that
for all u \in \mathbb{R}^{+}.
The graphs of the functions W and V are shown respectively in Figures 1 and 2.
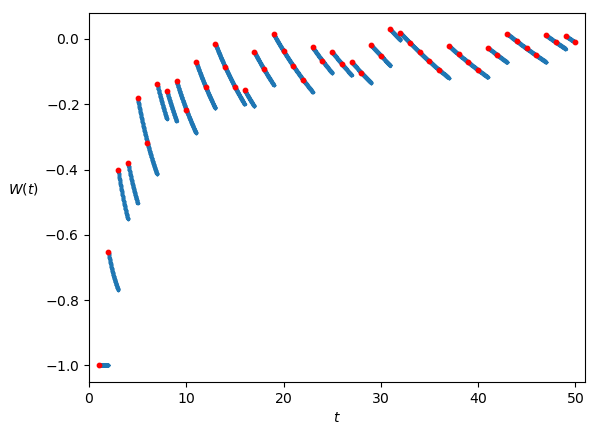
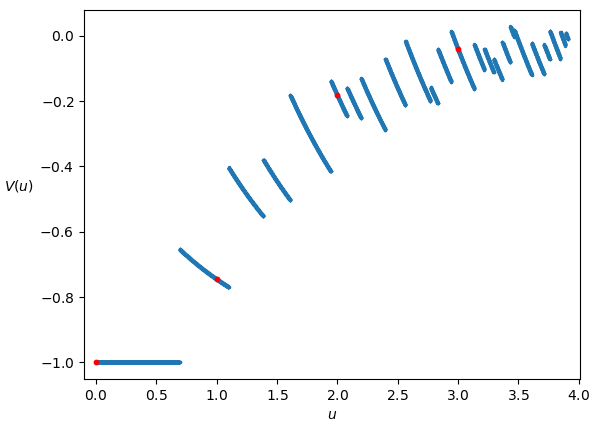
In the final part of the proof we’ll study these graphs in depth; for now we’ll limit ourselves to note some simple things:
- The graph of W has some discontinuities in correspondence with the integers for which the function \overline{\psi} changes value. For example, for t=1, \ldots, 6 we’ll have that \overline{\psi}(t) = \psi(t) = \log 1, \log 2, \log 6, \log 12, \log 60, \log 60, so \overline{\psi} changes value in the passage from 1 to 2, from 2 to 3, from 3 to 4, from 4 to 5, but it remains constant when passing from 5 to 6. In the graph (Figure 1), you can see this because there are discontinuities in the points 2, 3, 4, and 5, but not in the point 6. In fact the points 5 and 6 graphically lay on the same continuous segment.
- From one integer up to but not including the next one, the function W is strictly decreasing.
- The graph of V between two integers n and n + 1 reproduce the graph of W between e^n and e^{n + 1}. Figure 3 shows this for n = 1.
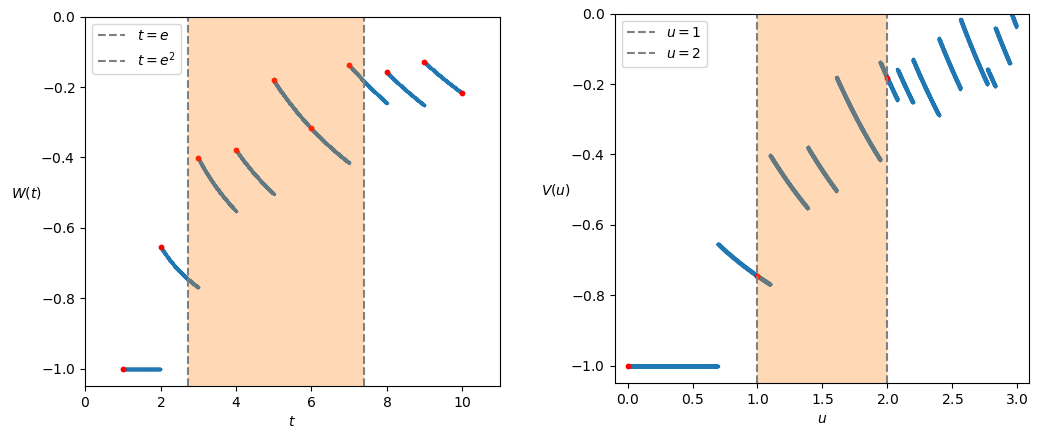
The first two points, in particular, are the basis for the proof of the following Proposition:
The functions |W| and |V| are bounded
The functions |W| and |V| are bounded.
We can note that, by Definition N.13:
So, in order to prove that |W| is bounded, we have to prove that the function \left| \frac{\overline{\psi}(t)}{t} \right| is bounded. We can note that this function is equal to \frac{\overline{\psi}(t)}{t}: we can get rid of the absolute value, because both \overline{\psi}(t) and t are non-negative; so we have to prove that the function \frac{\overline{\psi}(t)}{t} is bounded.
First of all, for integer values of t, we can apply Theorem N.4, by which \psi(t) \asymp t. By Definition A.3, this means that there exists a real positive constant A such that definitively |\psi(t)| \leq At; hence, being \psi non-negative, \psi(t) \leq At, i.e. \frac{\psi(t)}{t} \leq A. But, still limitating ourselves to integer values of t, if the last inequality is true definitively, i.e. for every t greater or equal to some fixed t_0, then a similar inequality is also true for all t. In fact, the set of numbers \left\{\frac{\psi(1)}{1}, \frac{\psi(2)}{2}, \ldots, \frac{\psi(t_0 - 1)}{t_0 - 1}\right\}, being finite, has a maximum value M, so for t \lt t_0 we’ll have that \frac{\psi(t)}{t} \leq M, and generally, considering also the case of t \geq t_0, we’ll have that \frac{\psi(t)}{t} \leq \max(M, A). So the function \frac{\psi(t)}{t}, for integer values of t (and so coinciding with \frac{\overline{\psi}(t)}{t}), is bounded.
Now let’s see what happens for non-integer values of t. In particulat, let’s focus our attention on the intervals of the kind (n, n+1), where n is a positive integer. In these intervals, by definition of simple extension, the function \overline{\psi} is constant and equal to \psi(n), so for t \in (n, n+1) we’ll have that \frac{\overline{\psi}(t)}{t} = \frac{\psi(n)}{t} \lt \frac{\psi(n)}{n}. But, by the previous part, \frac{\psi(n)}{n} \leq \max(M, A), so \frac{\overline{\psi}(t)}{t} \leq \max(M, A) in all the intervals of the kind (n, n+1) and, including n, also in all the intervals of the kind [n, n+1). But, for n \geq 1, the union of such intervals covers all the function domain, which is the same as W i.e. [1, +\infty), so we can say that \frac{\overline{\psi}(t)}{t} \leq \max(M, A) for all t. So the function \frac{\overline{\psi}(t)}{t} is bounded, that is what we wanted to prove.
The boundedness of the function |V| is now an immediate consequence, since |V(u)| = |W(e^u)| \leq \max(M, A), for all u.
Definition N.13 lets us rewrite (4) like this:
Now let’s analyze the functions W and V in a greater depth.
The function W computes a relative error. In fact the numerator \overline{\psi}(t) - t is an extension of the function \psi(x) - x, which represents the difference between the quantity we want to approximate and the asymptotic estimate we want to obtain, by (3). The function W however does not express this difference by itself, but with respect to the value of x (which after the extension to real numbers becomes t). This is a general principle which is applied when a relative error is computed. For example, making an error of a unity in one thousand is different from making an error of a unity in one million: the relative error is one thousandth in the first case, one millionth in the second case.
So the relative error is a function that indicates rather intuitively the similarity between two values, in this case \overline{\psi}(t) and t. By (3′), we have to prove that there is a certain similarity between these two functions (that is the asymptotic equivalence) and so, intuitively, we can expect the relative error W(t) = \frac{\overline{\psi}(t) - t}{t} to tend to zero. Indeed, the two things are equivalent:
So we rephrased further our goal, that from (3) can be rewritten equivalently like this:
But, by Definition N.13, W(x) = W(\exp(\log x)) = V(\log x), hence:
Thus we have obtained a further reformulation of our goal:
Summarizing, we have the following chain of implications (that are actually double implications) that bring us towards the Prime Number Theorem:
So we reduced the proof of the Prime Number Theorem to the problem of proving that \lim_{x \to +\infty} V(\log x) = 0. Careful, because in this statement it’s implied that the limit exists, besides being 0; the limit existence is always part of the thesis to be proved. So, how to prove that the limit of a function exists and is 0?
The most immediate method is to apply Proposition A.2 (Every real sequence having \liminf equal to \limsup has a limit), according to which:
That is, for proving that the limit of V exists and is 0, it should be proved that the limit inferior and the limit superior of the function are equal to zero too. The advantage of this technique is that the limit superior and the limit inferior, unlike the limit, always exist by definition; they just have to be computed (admitting as possible values also \pm \infty). So (5) lets us establishing the numerical value and the existence of a single object (the limit of V) on the basis of the numerical value of two distinct objects (its limit superior and inferior), of which however we have not to care about the existence. We can say that it’s a good simplification. The drawback is that now we have two equations that we should study separately: \limsup_{x \to +\infty} V(\log x) = 0 and \liminf_{x \to +\infty} V(\log x) = 0. In principle, after having proved one of the two, the proof should be restarted from the beginning in order to prove also the other one. But here it’s possible to simplify again, joining the two equations into a single one. In fact, it can be proved that:
>In this detail we’ll denote for the sake of brevity \limsup_{x \to +\infty} V(\log x) and \liminf_{x \to +\infty} V(\log x) simply as \limsup V and \liminf V. Let’s start to prove the implication towards right: \limsup V = \liminf V = 0 \Rightarrow \limsup |V| = 0.
Getting back to formula (5), we have that, if \limsup V = \liminf V = 0, than the function V tends to zero. But if V tends to zero, its opposite -V tends to zero too (by the definition of limit, or because \lim -V = -\lim V = -0 = 0), so its absolute value tends also to zero, by the so called “Squeeze Theorem“, being always -V \leq |V| \leq V. Summarizing, 0 = \lim V = \lim -V = \lim |V|. But if \lim |V| = 0, then, by the aforementioned Proposition A.2, \limsup |V| = \liminf |V| = 0; in particular \limsup |V| = 0, that is what we wanted to prove.
Conversely, if \limsup |V| = 0, being always V \leq |V|, by the definition of limit superior (and as it’s easy to realize), we’ll have that \limsup V \leq \limsup |V|, hence:
We can note that, being |V| = |-V|, we can put -V in place of V in all the previous passages, up to formula (7), obtaining:
Now we can employ a general property that connects the limit superior and the limit inferior, which in our case translates into the equality \limsup -V = -\liminf V, from which, by (7′), -\liminf V \leq 0, hence:
Joining (7) and (8), we’ll have that \limsup V \leq 0 \leq \liminf V, so \limsup V \leq \liminf V. But we know that the inverse relationship is generally true, that is \liminf V \leq \limsup V; so in this case, being both relationships true, we must have that \liminf V = \limsup V. In addition, again by (7) and (8), we can extend this inequality, obtaining 0 \leq \liminf V = \limsup V \leq 0, and so \liminf V = \limsup V = 0, that is what we had to prove.
So, provided that the absolute value has been introduced, it’s possible to come back to a single equation, like when there was the limit, but with the advantage of the \limsup, that consists in existing always. Of course, the absolute value is not easy to work with, but we’ll be able to develop most of the proof without it, and we’ll introduce it only when necessary.
Now, since we made several backward steps in order to obtain simpler and simpler formulas, it’s worth stopping for a while for summarizing, travelling through the passages again onwards. Concerning our goal, in order to achieve the Prime Number Theorem formula we travelled through the following chain of implications (which are indeed double implications, but this is not important for the proof):
This chain of implications proves the following Lemma, according to which in the following posts we’ll be allowed to forget the passages above, in order to focus our attention on the proof of the formula \limsup_{x \to +\infty} |V(\log x)| = 0:
Sufficient condition for the validity of the Prime Number Theorem
The following is a sufficient condition for the validity of the Prime Number Theorem:
where the function V is defined in Definition N.13.
Our starting point was also the object of some backward passages, which let us introduce the function V and can be summarized as follows:
So, substantially, if we prove the implication:
we would prove the Prime Number Theorem. In fact, the previous passages and formula (2) prove the truth of the left part, while Lemma N.7 guarantees the sufficiency of the right part; what’s missing is to prove the implication.
In the next post we’ll see how, starting from (9), is possible to sketch out the continuation of the proof.