Prerequisiti:
- Calcolo della riga per i tratteggi lineari di secondo ordine
- Periodicità e simmetria nei tratteggi lineari
- Definizioni e simboli di teoria dei tratteggi
Anche per il calcolo della riga dell’x-esimo trattino per i tratteggi lineari di terzo ordine, come per il secondo, esistono dei particolari moduli che, valutando delle opportune condizioni, ci danno informazioni sull’appartenenza ad una certa riga i. Tuttavia rispetto al secondo ordine vi sono anche delle importanti differenze:
- La complessità dei calcoli: il calcolo manuale della riga può richiedere qualche minuto;
- La generalità: esiste una condizione semplice per il calcolo della riga, ma vale solo per i tratteggi le cui componenti sono a due a due coprime. Se si vuole effettuare il calcolo in generale, vanno gestiti dei casi particolari che a volte possono verificarsi.
Questi problemi, in realtà, non sono così gravi come possono sembrare. La complessità dei calcoli non rappresenta un problema se si usa un computer, nè preclude l’importanza teorica dei risultati. Anche il calcolo matriciale, per esempio, è ostico da svolgere manualmente già per matrici di piccoli ordini, ma questo non sminuisce l’importanza delle matrici nelle applicazioni, né fa perdere valore alla teoria dell’algebra lineare sottostante. Per quanto riguarda la generalità, come vedremo nella sezione relativa alle applicazioni della teoria dei tratteggi, i tratteggi che ci interessano per lo studio dei numeri primi sono quelli che hanno come componenti a loro volta numeri primi; essendo tali, le componenti di questi tratteggi sono a maggior ragione a due a due coprime, quindi si può usare la condizione più semplice per il calcolo della riga.
Nel seguito vedremo tutto ciò nel dettaglio. Le dimostrazioni sono in Teoria dei tratteggi, pagg. 163-172.
Tratteggi con componenti a due a due coprime
Vediamo cosa accade nei tratteggi le cui componenti sono a due a due coprime, che costituiscono, come abbiamo detto, il caso più semplice. Consideriamo a titolo di esempio il tratteggio di terzo ordine di questo genere con le componenti più piccole possibile, ossia (2, 3, 5):
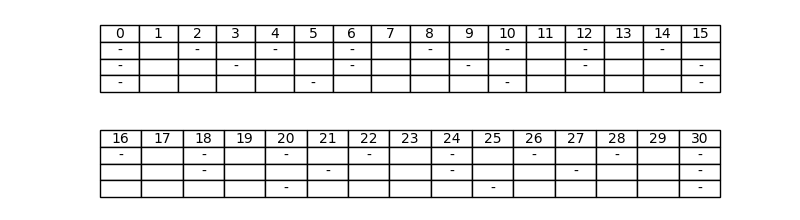
Come per il secondo ordine, anche per il terzo vi è un modulo che caratterizza ciascuna riga. Per la prima riga, indicando il tratteggio con T = (n_1, n_2, n_3), è questo:
Osserviamo una prima analogia col secondo ordine: i moduli che compaiono nel Teorema T.2 (Calcolo della riga dell’x-esimo trattino in un tratteggio lineare di secondo ordine) vengono calcolati rispetto ad n_1 + n_2, che dal punto di vista algebrico è un polinomio simmetrico rispetto ad entrambe le variabili n_1 ed n_2. Analogamente, il modulo (1) è calcolato rispetto al polinomio n_1 n_2 + n_1 n_3 + n_2 n_3 che è simmetrico rispetto a n_1, n_2 ed n_3. Ma abbiamo già incontrato questi polinomi parlando della periodicità dei tratteggi lineari. In particolare, per il Corollario della Proprietà T.4 (Numero di trattini di un periodo di un tratteggio lineare con componenti a due a due coprime), questi sono i polinomi che contano il numero di trattini in un periodo di un tratteggio lineare con componenti a due a due coprime. Per questo Corollario, la formula che calcola il numero di trattini in un periodo quando l’ordine è k = 3 è proprio n_1 n_2 + n_1 n_3 + n_2 n_3, mentre per k = 2 è n_1 + n_2.
Torniamo ora al modulo (1). Dato che il polinomio n_1 n_2 + n_1 n_3 + n_2 n_3 ricorrerà spesso e, come abbiamo appena visto, è molto significativo, conviene dargli un nome. Lo chiameremo N:
Con questa notazione, il modulo (1) si riscrive come:
Eseguendo i calcoli per il tratteggio T = (n_1, n_2, n_3) = (2, 3, 5) della Figura 1, si ha N = 2 \cdot 3 + 2 \cdot 5 + 3 \cdot 5 = 31 e la (3) diventa (3 + 5) 2 x \mathrm{\ mod\ } N = 16 x \mathrm{\ mod\ } 31. Calcoliamo ora questo modulo per ogni ordinale x:
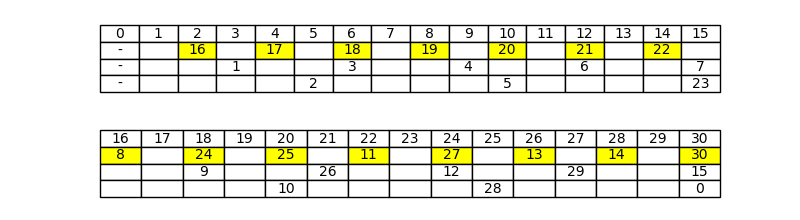
I numeri sulla prima riga, evidenziati in giallo, costituiscono un insieme ben preciso, che chiameremo R_T(1). Esso si ottiene, nel caso di un tratteggio T = (n_1, n_2, n_3) con componenti a due a due coprime, come segue:
Nel caso del tratteggio (2, 3, 5), eseguendo i calcoli si ha:
Se si osserva la Figura 2, si può vedere che questi sono esattamente i valori del modulo (3) riportati sulla prima riga. Infatti in generale si dimostra che:
Un discorso analogo vale per le altre righe. Per valutare l’appartenenza dell’x-esimo trattino alla seconda riga, il modulo da valutare è il seguente:
Eseguendo i calcoli per (n_1, n_2, n_3) = (2, 3, 5), questa formula diventa (2 + 5) 3 x \mathrm{\ mod\ } N = 21 x \mathrm{\ mod\ } 31. Calcoliamo questo modulo per ogni ordinale x del tratteggio (2, 3, 5):
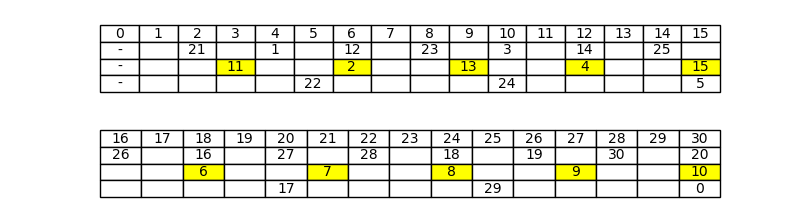
I numeri presenti sulla seconda riga, evidenziati in giallo, costituiscono il seguente insieme, che chiameremo R_T(2):
Nel caso del tratteggio (2, 3, 5), eseguendo i calcoli si ottiene:
E questi sono esattamente i valori presenti nella seconda riga della Figura 3. In generale:
Per quanto riguarda la terza riga, il modulo da calcolare è:
Nel tratteggio (2, 3, 5) esso diventa (2 + 3) 5 x \mathrm{\ mod\ } N = 26 x \mathrm{\ mod\ } 31 ed assume i seguenti valori:
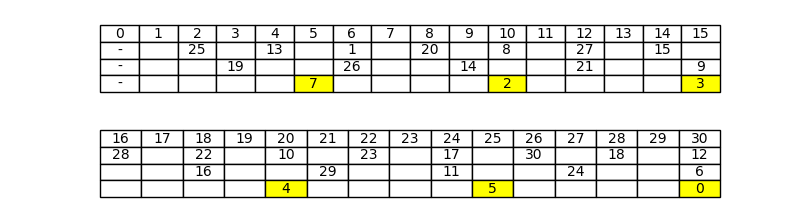
I numeri sulla terza riga, evidenziati in giallo, costituiscono l’insieme R_T(3) definito da:
che nel caso che stiamo esaminando diventa:
Questa volta la condizione che caratterizza l’appartenenza alla terza riga è la seguente:
Si può trovare riscontro di questo nella Figura 4.
Notiamo che le definizioni degli insiemi R_T(1), R_T(2) ed R_T(3) (formule (4), (7) e (9)), sono simili ma presentano delle differenze riguardo a quali componenti sono presenti e a come variano i numeri a e b per cui esse sono moltiplicate. Anche le formule (5), (8) e (10), che caratterizzano l’appartenenza ad una riga, presentano una forte somiglianza nella struttura, ma le componenti risultano scambiate di posto tra una formula e l’altra. Analizzando queste differenze è possibile ottenere un’unica formula più generale sia per gli insiemi R_T(i), sia per la caratterizzazione dell’appartenenza alla generica riga i, al variare di i.
Le regole generali che stanno alla base della definizione dell’insieme R_T(i), per i = 1, 2, 3, sono le seguenti:
- Le componenti presenti sono quelle con indice diverso da i: nella definizione dell’insieme R_T(1) compaiono le componenti diverse da n_1; in quella di R_T(2) le componenti diverse da n_2; in quella di R_T(3) le componenti diverse da n_3.
- Ciascuna delle componenti presenti viene moltiplicata per un numero che varia:
- Tra 1 e l’altra componente presente, se quest’ultima ha indice maggiore di i
- Tra 0 e l’altra componente presente meno uno, se quest’ultima ha indice minore di i
Infatti:
- In R_T(1) la componente n_2 è moltiplicata per un numero che varia tra 1 ed n_3, perché l’altra componente con indice diverso da 1 è n_3 e l’indice 3 è maggiore di 1; una cosa analoga vale per la componente n_3.
- In R_T(2) la componente n_1 è moltiplicata per un numero che varia tra 1 ed n_3, perché l’altra componente con indice diverso da 2 è n_3 e l’indice 3 è maggiore di 2; invece la componente n_3 è moltiplicata per un numero che varia tra 0 ed n_1 - 1, perché l’altra componente con indice diverso da 2 è n_1 e questa ha indice minore di 2.
- In R_T(3) la componente n_1 è moltiplicata per un numero che varia tra 0 ed n_2 - 1, perché l’altra componente con indice diverso da 3 è n_2 e l’indice 2 è maggiore di 1; una cosa analoga vale per la componente n_2.
In formule, si possono generalizzare le definizioni (4), (7) e (9) mediante la seguente, dove si assume che \{i, j, k\} = \{1, 2, 3\}:
Con la stessa assunzione su i, j e k, si possono anche generalizzare le formule (5), (8) e (10) come segue:
Possiamo ricapitolare quanto visto fin qui nel seguente Teorema:
Calcolo della riga dell’x-esimo trattino in un tratteggio lineare di terzo ordine con componenti a due a due coprime
Sia T un tratteggio lineare di terzo ordine avente indici I = \{1, 2, 3\}, le cui componenti sono a due a due coprime. Siano \{i, j, k\} = \{1, 2, 3\}. Allora per ogni x \gt 0:
Dove N := n_1 n_2 + n_1 n_3 + n_2 n_3 ed R_T(i) è definito da:
In particolare, per i singoli valori possibili di i, i = 1, 2, 3, si ha:
Dove
Applicando il Teorema T.4, stabiliamo a quale riga appartiene il sesto trattino del tratteggio T = (2, 3, 5) visualizzato in Figura 1.
Vediamo se appartiene alla prima riga. Dobbiamo allora calcolare il modulo (n_2 + n_3) n_1 x \mathrm{\ mod\ } N della formula (3), ossia 16 x \mathrm{\ mod\ } 31, che per x = 6 assume il valore 96 \mathrm{\ mod\ } 31 = 3. Per le formule (5) e (4), il sesto trattino appartiene alla prima riga se e solo se il numero 3 appartiene a R_{(2,3,5)}(1), cioè se può essere scritto nella forma
Ma questo non è possibile. Si può scrivere ad esempio 3 = 3 \cdot 1 + 5 \cdot 0, ma 0 \notin \{1, 2, 3\}. In effetti, il più piccolo numero che si può scrivere come 3 a + 5 b, dovendo essere sia a che b positivi, si ottiene assegnando alle due variabili i valori più piccoli possibili, in questo caso a = 1 e b = 1. Ma così facendo otteniamo 3 \cdot 1 + 5 \cdot 1 = 3 + 5 = 8, che è maggiore di 3, pur essendo il numero più piccolo che soddisfa i nostri vincoli. Quindi 3 è troppo piccolo per essere espresso nella forma (11), e quindi per il Teorema T.4 concludiamo che il sesto trattino non appartiene alla seconda riga.
Vediamo allora se il sesto trattino appartiene alla seconda riga. In questo caso dobbiamo calcolare il modulo (n_1 + n_3) n_2 x \mathrm{\ mod\ } N della formula (6), ossia 21 x \mathrm{\ mod\ } 31, che per x = 6 assume il valore 126 \mathrm{\ mod\ } 31 = 2. Per le formule (8) e (7), il sesto trattino appartiene alla seconda riga se e solo se il numero 2 può essere scritto nella forma
Anche in questo caso 2 è un numero molto piccolo, perciòla soluzione va ricercata tra i più piccoli valori leciti di a e di b. In effetti la soluzione si ha proprio per a = 1 e b = 0:
Dunque la (12) ha soluzione, e per il Teorema T.4 possiamo dire che il sesto trattino appartiene alla seconda riga, come possiamo vedere, contando i trattini di valore positivo, in Figura 1.
Naruralmente, se provassimo a verificare l’appartenenza alla terza riga, otterremmo un’altra equazione che non ha soluzione, come è accaduto per la prima riga.
Come abbiamo visto nel precedente esempio, il calcolo della riga nei tratteggi di terzo ordine si riconduce alla risoluzione di equazioni del tipo
nelle incognite a e b, dove c_1, c_2 e c_3 sono costanti e sia le costanti che le incognite sono numeri interi. Si tratta delle cosiddette equazioni diofantee, ma nel nostro caso, a differenza della teoria classica delle equazioni diofantee, non possiamo accettare tutte le soluzioni, ma solo quelle che rispettano dei particolari vincoli su a e b. Ad esempio, prendendo spunto dalla formula (11), possiamo richiedere che a e b siano tali che:
Per quanto ne sappiamo, non esistono studi su equazioni diofantee soggette a vincoli di questo tipo. Perciò, per il momento, il miglior metodo risolutivo è ragionare su casi specifici, come nell’esempio precedente, oppure possiamo semplicemente procedere per tentativi. In ogni caso, riteniamo che sia interessante aver trovato questo collegamento tra due teorie apparentemente distanti, quella dei tratteggi e quella delle equazioni diofantee. Magari in futuro i risultati di una delle due teorie potranno essere applicati anche nell’altra.
Tratteggi generici
Vediamo come cambia il calcolo della riga per i tratteggi lineari di terzo ordine quando le componenti non sono necessariamente a due a due coprime, ma possono essere qualsiasi.
In questo caso continua a valere l’implicazione verso destra del Teorema T.4, cioè se l’x-esimo trattino appartiene alla riga di indice i, allora il modulo della formula (5 + 8 + 10) appartiene all’insieme R_T(i). Tuttavia l’implicazione non vale nel senso opposto: se il modulo appartiene all’insieme R_T(i), esistono dei casi particolari in cui il trattino appartiene ad una riga con indice diverso da i, come asserito dal seguente Teorema.
Calcolo della riga dell’x-esimo trattino in un tratteggio lineare di terzo ordine qualsiasi
Sia T un tratteggio lineare di terzo ordine avente indici I = \{1, 2, 3\}. Allora per ogni x \gt 0:
Dove N ed R_T(i) sono definiti come nel Teorema T.4.
Viceversa, se (n_j + n_k) n_i x \mathrm{\ mod\ } N \in R_T(i) per qualche i, indicando con t il trattino \mathrm{t}_T(x) e con v il suo valore, possono verificarsi i seguenti casi:
- Se n_2 \nmid v oppure se i = 2, allora t \in T[i]
- Altrimenti:
- Se i = 1 e n_2 n_3 = (n_2 + n_3)(n_1 - v \mathrm{\ mod\ } n_1), allora:
\begin{cases} t \in T[3] & \text{se } (n_2 + n_3) n_1 x \mathrm{\ mod\ } N = 2 n_2 n_3 \\ t \in T[1] & \text{altrimenti} \end{cases} \tag{14}
- Se i = 3 e n_1 n_2 = (n_1 + n_2)(n_3 - v \mathrm{\ mod\ }^{\star} n_3), allora:
\begin{cases} t \in T[3] & \text{se } (n_1 + n_2) n_3 x \mathrm{\ mod\ } N = 0 \\ t \in T[1] & \text{altrimenti} \end{cases} \tag{15}
- In tutti gli altri casi, t \in T[i]
- Se i = 1 e n_2 n_3 = (n_2 + n_3)(n_1 - v \mathrm{\ mod\ } n_1), allora:
La cosa più importante da ricordare di questo Teorema è che l’implicazione della (5 + 8 + 10 bis) vale anche verso sinistra:
- Se i = 2, sempre
- Se i = 1 o i = 3, almeno quando n_2 non divide v, cioè quando non vi è un trattino della riga 2 sulla stessa colonna di t
I casi particolari che intervengono quando queste condizioni non sono verificate sono abbastanza rari nella pratica.
Si può osservare che il Teorema T.4 è di fatto un corollario del Teorema T.6 (anche se per questioni di ordine espositivo abbiamo preferito presentarli entrambi come teoremi). Infatti, gli unici casi in cui l’implicazione della (5 + 8 + 10 bis) non vale anche verso sinistra, cioè i casi in cui (n_j + n_k) n_i x \mathrm{\ mod\ } N \in R_T(i) ma t \notin T[i], si verificano quando:
In particolare, perché queste condizioni siano verificate, è necessario che lo siano anche le seguenti:
Infatti, per i = 1, se n_2 + n_3 non divide n_2 n_3, quest’ultimo non potrebbe essere scritto come (n_2 + n_3)(n_1 - v \mathrm{\ mod\ } n_1), ossia come un prodotto in cui uno dei fattori è proprio n_2 + n_3, quindi il primo caso della (16) non può essere vero, essendo una congiunzione logica (un “and”) di due condizioni la prima delle quali è falsa; analogamente ragionando per i = 3.
Ma le condizioni (17) non possono verificarsi se n_1, n_2 ed n_3 sono a due a due coprimi. Il motivo è che la somma di due numeri coprimi è coprima con ciascuno di essi, e quindi anche col loro prodotto; ma se è coprima col loro prodotto, certamente non può dividerlo. Nel nostro caso, se i = 1 ed n_2 ed n_3 sono coprimi, allora n_2 + n_3 è coprimo sia con n_2 che con n_3, quindi anche con n_2 n_3, perciò non può dividere n_2 n_3, come dovrebbe essere nel primo caso della (17). Analogamente si può ragionare per i = 3.
L’enunciato del Teorema T.6 è difficilmente applicabile nella pratica, perché i criteri necessari per verificare l’appartenenza ad una riga spesso coinvolgono v, che normalmente non è noto a priori. Comunque, in linea con l’osservazione precedente, pensiamo che esso possa essere semplificato togliendo i riferimenti a v, ad esempio l’ultima parte dell’enunciato potrebbe diventare:
- Se i = 2, allora t \in T[i]
- Altrimenti:
- Se i = 1 e (n_2 + n_3) \mid n_2 n_3, allora
\begin{cases} t \in T[3] & \text{se } (n_2 + n_3) n_1 x \mathrm{\ mod\ } N = 2 n_2 n_3 \\ t \in T[1] & \text{altrimenti} \end{cases}
- Se i = 3 e (n_1 + n_2) \mid n_1 n_2, allora
\begin{cases} t \in T[3] & \text{se } (n_1 + n_2) n_3 x \mathrm{\ mod\ } N = 0 \\ t \in T[1] & \text{altrimenti} \end{cases}
- In tutti gli altri casi, t \in T[i]
- Se i = 1 e (n_2 + n_3) \mid n_2 n_3, allora
Questo però deve essere verificato ed, eventualmente, dimostrato.
Completiamo questo paragrafo con un esempio di quando l’implicazione della (5 + 8 + 10 bis) non vale verso sinistra. A tale scopo consideriamo il tratteggio (5, 3, 6) ed il suo dodicesimo trattino, che chiameremo t:
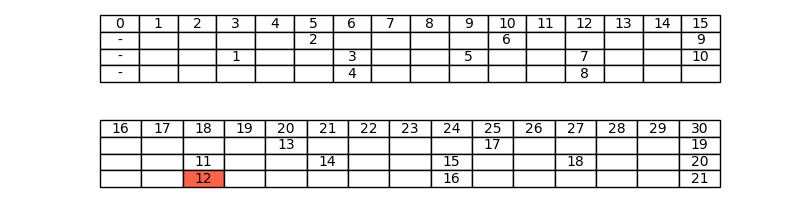
Calcoliamo innanzitutto gli insiemi R_T(i) per tutti gli indici di riga:
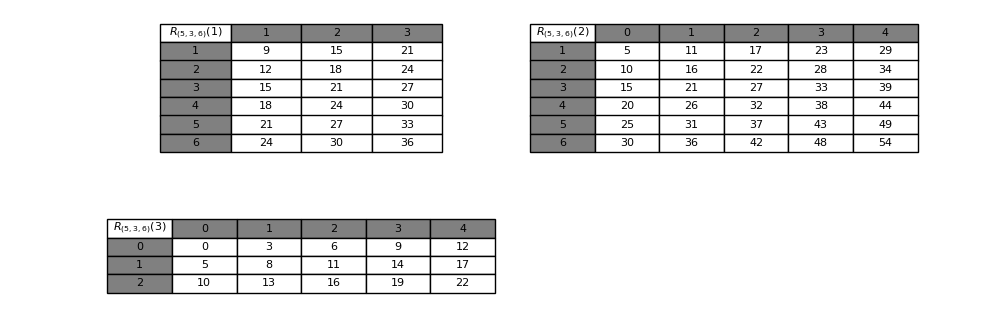
Ora, posto che N = n_1 n_2 + n_1 n_3 + n_2 n_3 = 5 \cdot 3 + 5 \cdot 6 + 3 \cdot 6 = 63, per il Teorema T.6 dobbiamo chiederci: (n_j + n_k) n_i x \mathrm{\ mod\ } N, per x = 12, appartiene a R_T(i) per qualche i?
Cominciamo da i = 1. In questo caso il modulo diventa:
Come si può vedere in Figura 6, il modulo 36 compare in R_T(i) = R_T(1), ma compare anche in R_T(2). Questo fatto di per sé è già sufficiente per dire che l’implicazione della (5 + 8 + 10 bis) non vale verso sinistra, perché il modulo appartiene ad R_T(i) per diversi i: se l’implicazione valesse verso sinistra, il trattino t si troverebbe contemporaneamente sulla riga di indice 1 e su quella di indice 2, il che sarebbe assurdo. Vediamo allora come, applicando il Teorema T.6, è possibile risolvere questa ambiguità sulla riga.
Innanzitutto, guardando la Figura 5 sappiamo che il valore di t è v = 18, che è multiplo di n_2 = 3, quindi non si verifica nessuna delle due condizioni n_2 \nmid v \Rightarrow 3 \nmid 18 oppure i = 2, che garantirebbero l’appartenenza alla riga T[i] = T[1]. Inoltre ci troviamo proprio nel caso in cui n_2 n_3 = (n_2 + n_3)(n_1 - v \mathrm{\ mod\ } n_1): infatti n_2 n_3 = 18 e (n_2 + n_3)(n_1 - v \mathrm{\ mod\ } n_1) = (3 + 6)(5 - 18 \mathrm{\ mod\ } 5) = 9(5 - 3) = 18. Allora per stabilire a quale riga appartiene t dobbiamo applicare la formula (14), ossia stabilire se il modulo (n_2 + n_3) n_1 x \mathrm{\ mod\ } N è uguale a 2 n_2 n_3 = 2 \cdot 3 \cdot 6 = 36. In effetti è proprio così (v. formula (18)), quindi per la (14) si ha che t \in T[3], che è il risultato corretto, come si può vedere in Figura 5.
Come abbiamo osservato in precedenza, per applicare il Teorema T.6 è stato necessario conoscere v, e noi lo conoscevamo perché avevamo già disegnato la tabella del tratteggio. Tuttavia per lo stesso motivo vedevamo anche che il trattino appartiene alla terza riga, senza aver applicato il Teorema T.6. Comunque, se fosse vera la versione semplificata che abbiamo visto nell’osservazione precedente, avremmo potuto stabilire a quale riga appartiene il trattino senza aver prima disegnato la tabella, valutando semplicemente la condizione (n_2 + n_3) \mid n_2 n_3, che è vera perché n_2 + n_3 = 3 + 6 = 9 divide n_2 n_3 = 3 \cdot 6 = 18.
Siamo arrivati a dire che t \in T[3] partendo da i = 1, ma questa scelta di i è stata arbitraria: cosa sarebbe successo scegliendo altri i?
Vediamo per i = 2. In questo caso dobbiamo valutare il modulo della formula (8):
Questo numero si trova solo in R_T(1). Dovremmo concludere allora che t \in T[1]? No, perché la condizione da valutare è
Mentre in questo caso i = 2 e (n_1 + n_3) n_2 x \mathrm{\ mod\ } N \notin R_T(2): se non accade questo non possiamo andare avanti, non importa se il modulo appartiene a qualche altro R_T(\cdot). In questo caso, l’unica informazione che riusciamo ad avere sulla riga è che t \notin T[2]. Possiamo dedurre questo applicando la negazione della (5 + 8 + 10 bis): infatti, se t appartenesse a T[2], il modulo (n_1 + n_3) n_2 x \mathrm{\ mod\ } N apparterrebbe a R_T(2); ma se così non è, vuol dire che t \notin T[2].
Se invece fossimo partiti da i = 3, avremmo ottenuto:
che si trova in R_T(i) = R_T(3), ma anche in R_T(1). In questo caso però non è vero che n_1 n_2 = (n_1 + n_2)(n_3 - v \mathrm{\ mod\ }^{\star} n_3), infatti n_1 n_2 = 5 \cdot 3 = 15 e n_3 - v \mathrm{\ mod\ }^{\star} n_3 = 6 - 18 \mathrm{\ mod\ }^{\star} 6 = 6 - 6 = 0, quindi il loro prodotto è 0. Allora ci dobbiamo fermare, perché non ci sono le premesse per valutare la condizione (15). Diversamente dal caso di i = 2, in questo caso non abbiamo nessuna informazione sulla riga di t, nemmeno sulla non-appartenenza ad una riga.
Concludendo, l’unico i che ci permette di calcolare la riga di t è i = 1. È interessante notare che ciò accade sebbene il trattino non appartenga alla riga di indice 1, ma questo fa parte delle “stranezze” del Teorema T.6 rispetto al molto più semplice Teorema T.4. Nonostante casi come questo siano rari nella pratica, grazie a questo esempio possiamo avere un’idea delle complicazioni che si evitano quando si suppone che un tratteggio abbia componenti a due a due coprime.