Prerequisiti:
- La seconda parte della dimostrazione del Teorema dei numeri primi: le idee di partenza
- Fine della prima parte della dimostrazione: la relazione tra α e β’
- Le funzioni W e V
- Proprietà degli ordini asintotici
In questo articolo completeremo la dimostrazione del Teorema dei numeri primi, applicando le idee fondamentali illustrate nell’articolo precedente. Suddivideremo quest’ultima parte della dimostrazione in cinque parti:
- Il nostro punto di partenza sarà una semplice maggiorazione dell’integrale di |V| in un intervallo qualsiasi, ottenuta applicando la Proprietà A.18;
- Miglioreremo il risultato del punto precedente supponendo che nell’intervallo la funzione V abbia almeno uno zero;
- Miglioreremo il risultato del primo punto anche per gli intervalli in cui la funzione V non ha zeri;
- Calcoleremo quale dovrebbe essere l’ampiezza \delta di un generico intervallo nel quale sia possibile applicare, a seconda dei casi, una o l’altra delle due maggiorazioni precedenti;
- Per finire, applicheremo i risultati precedenti all’intervallo [0, \log \xi] e otterremo il risultato finale facendo tendere \xi a +\infty.
Maggiorazione mediante il limite superiore
Come abbiamo visto nell’articolo precedente, il problema principale della seconda parte della dimostrazione del Teorema dei numeri primi consiste nel maggiorare l’integrale di |V| nell’intervallo [0, \log \xi] (dove \xi è la variabile utilizzata nel calcolo dei limiti superiori, ad esempio nella definizione di \alpha^{\prime} e \beta^{\prime}). Come abbiamo visto nella seconda idea, per effettuare questa operazione conviene suddividere questo intervallo in intervalli più piccoli. Allora, per il momento astraiamoci dall’intervallo originale (che non è fisso, ma dipende da \xi) e supponiamo di partire da un generico intervallo [a, a + \delta], ovviamente con \delta \gt 0 e a \geq 0. Cercheremo di trovare un valore di \delta che consente di effettuare una buona maggiorazione e vedremo che questa maggiorazione dipenderà solo da \delta, non da a.
Un modo molto semplice di maggiorare l’integrale di |V| nell’intervallo [a, a + \delta] consiste nell’applicare la Proprietà A.18, secondo cui:
Ma il termine tra parentesi è per definizione \alpha^{\prime}, quindi:
Applicando questa disuguaglianza nell’integrale, abbiamo che:
L’ultimo passaggio si giustifica come segue:
dove il passaggio (*) è del tutto analogo a quello applicato nella formula (9) dell’articolo precedente.
Nel seguito chiameremo la (1) “maggiorazione mediante il limite superiore”. Non è una maggiorazione molto raffinata, perché si basa su di una proprietà che vale in generale per le funzioni reali (la Proprietà A.18), non specifica per la funzione |V|. Nei paragrafi seguenti vedremo come, utilizzando invece alcune proprietà della funzione |V|, riusciremo ad ottenere una maggiorazione migliore.
Intervalli in cui V ha uno zero
Supponiamo che nell’intervallo [a, a + \delta] la funzione V abbia almeno uno zero (è un caso possibile perché la funzione V ha degli zeri, come è abbastanza evidente dalla Figura 2 dell’articolo precedente). Se indichiamo questo zero con t, per la Proposizione N.25 si ha che, per ogni h \geq 0:
Quindi, per la terza idea dell’articolo precedente, possiamo utilizzare questa disuguaglianza per maggiorare l’integrale della funzione |V| tra t e t + v, dove v è un numero reale positivo a nostra scelta:
Con un po’ di passaggi, si dimostra che:
Per prima cosa, dividiamo l’integrale in due parti:
La prima parte si sviluppa come segue:
Per quanto riguarda la seconda parte, dobbiamo considerare che la funzione che è argomento dell’O grande ha come variabile t, quindi è costante rispetto alla variabile di integrazione che è h. Perciò possiamo portare l’ordine asintotico fuori dall’integrale, ottenendo che \int_0^v O\left(\frac{1}{t}\right)\ dh = O\left(\frac{1}{t}\right) \int_0^v 1\ dh. Ora, l’integrale \int_0^v 1\ dh è pari a v, che è costante rispetto a t, quindi come ordine asintotico è O(1) per il Corollario della Proprietà A.7. Quindi abbiamo un O\left(\frac{1}{t}\right) che moltiplica un O(1), dando luogo, per la Proprietà A.8, a un altro O\left(\frac{1}{t}\right). Ma quest’ordine asintotico è un o(1) per la Proprietà A.16, perché \frac{1}{t} = o(1) per la Definizione A.4. In sintesi:
Sostituendo la (b) e la (c) nella (a) si ottiene:
Abbiamo dimostrato così il primo passaggio. Il secondo è una conseguenza della disuguaglianza v + \frac{1}{e^v} - 1 \leq \frac{v^2}{2}, che ora dimostriamo. Innanzitutto osserviamo che questa disuguaglianza è verificata per v \geq 2. In questo caso, infatti, \frac{1}{e^v} \lt 1, per cui v + \frac{1}{e^v} - 1 \leq v; inoltre v \leq \frac{v^2}{2}, perché \frac{v^2}{2} - v = \frac{v^2 - 2v}{2} = \frac{v(v - 2)}{2}, che è una quantità non negativa se v \geq 2. Vediamo quindi cosa succede per v \lt 2. A tal proposito, ricordiamo la serie di Maclaurin della funzione esponenziale:
da cui:
Ricordiamo che, per definizione di serie, il membro di destra è il limite della successione delle seguenti somme parziali (per semplicità utilizzeremo come indice iniziale 2):
Il limite di questa successione, per la (d), esiste ed è pari a v + \frac{1}{e^v} - 1.
Ora consideriamo la successione estratta b_j che si ottiene prendendo solo i termini di indice pari:
Analizziamo le differenze tra ciascun termine e il successivo:
Ora, per v \lt 2, tutti i fattori 1 - \frac{v}{4}, 1 - \frac{v}{6}, \ldots, 1 - \frac{v}{2j}, \ldots sono positivi; quindi, essendo anche v \gt 0, tutte le differenze b_2 - b_3, b_3 - b_4, \ldots, b_j - b_{j + 1}, \ldots sono positive. Ciò significa che per v \lt 2 la successione dei b_j è strettamente decrescente. Quindi tutti i termini della successione sono maggiorati dal primo termine, e questa proprietà si estende anche al limite:
Ma la successione (b_j) è stata estratta da (a_i), per cui deve avere lo stesso limite, che è pari alla somma della serie (d):
Unendo le formule (d), (e) ed (f), si ottiene infine:
Unendo le due formule precedenti, abbiamo che:
In questa disuguaglianza compare il termine asintotico o(1), che per il momento possiamo considerare come un termine di errore, di entità trascurabile perché tende a zero. Porteremo avanti questo errore fino alla fine, quando lo elimineremo grazie all’operazione di limite.
Il nostro scopo è rendere l’integrale della (2) più piccolo possibile, per cui, procedendo in analogia con le formule (3) e (7) dell’articolo precedente, dovremmo avere che:
dove \epsilon è un numero reale positivo fissato a priori, più piccolo possibile. Per fare in modo che valga quest’ultima disuguaglianza, per la (2) si deve avere che:
Quindi, per esempio, v potrebbe essere proprio uguale a \epsilon. Così si ottiene, sostituendo nella (2):
In pratica, così facendo abbiamo maggiorato l’integrale della funzione in un intervallo di ampiezza \epsilon, partendo da uno zero di V, con l’area di un triangolo rettangolo di base e altezza \epsilon, oppure di un rettangolo di base \epsilon e altezza \frac{\epsilon}{2}:
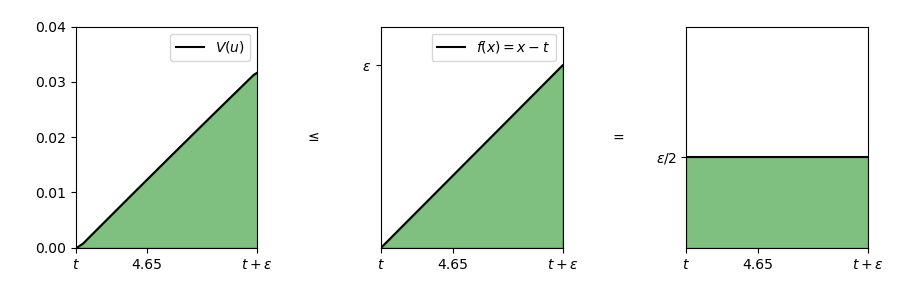
Finora abbiamo maggiorato l’integrale di |V| nell’intervallo [t, t + \epsilon], dove t è uno zero di V, mentre volevamo una maggiorazione nell’intervallo di partenza [a, a + \delta]. Possiamo raggiungere quest’obiettivo ragionando come segue:
- Supponiamo che \alpha^{\prime} \gt 0 e poniamo \epsilon := \alpha^{\prime}
- Supponiamo che [t, t + \alpha^{\prime}] \subseteq [a, a + \delta], ossia a \leq t \lt t + \alpha^{\prime} \leq a + \delta
La seconda supposizione è equivalente alla coppia di disuguaglianze a \leq t e t + \alpha^{\prime} \leq a + \delta, da cui a \leq t \leq a + \delta - \alpha^{\prime}. Quindi lo zero t non solo deve appartenere all’intervallo [a, a + \delta], come abbiamo supposto inizialmente, ma in particolare deve appartenere al sotto-intervallo [a, a + \delta - \alpha^{\prime}]. Quindi la seconda supposizione rende superflua l’ipotesi iniziale, perché la ingloba in sé (se V ha almeno uno zero in [a, a + \delta - \alpha^{\prime}], allora ha almeno uno zero in [a, a + \delta]). Naturalmente V potrebbe avere ulteriori zeri in [a + \delta - \alpha^{\prime}, a + \delta], ma non ci serve saperlo; l’importante è che ne abbia uno in [a, a + \delta - \alpha^{\prime}].
Un’altra conseguenza della seconda supposizione è che \delta \geq \alpha^{\prime}. Infatti, se l’intervallo [t, t + \alpha^{\prime}] è contenuto nell’intervallo [a, a + \delta], allora l’ampiezza di quest’ultimo, che è \delta, deve essere almeno pari all’ampiezza del primo, che è \alpha^{\prime}.
Con queste supposizioni, ragionando secondo la quarta idea dell’articolo precedente, possiamo estendere la maggiorazione dell’integrale dall’intervallo [t, t + \alpha^{\prime}] all’intervallo [a, a + \delta]. Applicando la maggiorazione del limite superiore e la formula (4) con \epsilon := \alpha^{\prime}, possiamo dimostrare il seguente Lemma:
Maggiorazione dell’integrale di |V| migliore di quella del limite superiore, primo caso
Supponiamo che \alpha^{\prime} \gt 0. Siano \delta \geq \alpha^{\prime} e a \geq 0. Se nell’intervallo [a, a + \delta - \alpha^{\prime}] la funzione |V| ha almeno uno zero, e se inoltre esiste una costante h \lt 1 tale che:
allora:
Sviluppando il termine a sinistra della disuguaglianza, otteniamo:
dove nel passaggio (*) abbiamo applicato la maggiorazione del limite superiore negli intervalli [a, a + t] e [t + \alpha^{\prime}, a + \delta], mentre nell’intervallo [t, t + \alpha^{\prime}] abbiamo applicato la (4) con \epsilon := \alpha^{\prime}.
Osserviamo che:
Unendo le due formule precedenti (g) e (h) si ottiene:
Rispetto alla (1), c’è il simbolo di minore invece che il simbolo di minore o uguale, quindi effettivamente quest’ultima è una maggiorazione migliore. Tuttavia, non possiamo accontentarci di questa lieve differenza. Infatti alla fine dovremo passare al limite ma, come è ben noto in analisi, se f \lt g allora \lim f \leq \lim g (ovviamente sotto le opportune ipotesi che rendono sensate le notazioni): il limite trasforma \lt in \leq, per cui ci ritroveremmo al punto di partenza. La soluzione però è semplice. Guardando attentamente la formula (h) si può notare che il segno di minore non riguarda in realtà tutta l’espressione, ma solo la parte senza l’ordine asintotico:
Equivalentemente, possiamo dire che esiste una costante h \lt 1 tale che:
La dimostrazione è così conclusa, perché la (5) è la sintesi di (g) e (j). Prima di chiudere il discorso, però, osserviamo la relazione che si ottiene eliminando il passaggio intermedio:
Questa relazione è preferibile rispetto alla (i), perché, trasformandola in limite, il simbolo di \leq viene mantenuto, così come la costante \delta h \alpha^{\prime}, ma \delta h \alpha^{\prime} \lt \delta \alpha^{\prime}; quindi, grazie a questa tecnica, riusciremo a conservare il segno di minore anche dopo aver essere passati al limite. Lo vedremo nel dettaglio nell’ultimo paragrafo.
Ora abbiamo maggiorato l’integrale della funzione in [a, a + \delta] con l’area di un rettangolo di base \delta e altezza h \alpha^{\prime}:
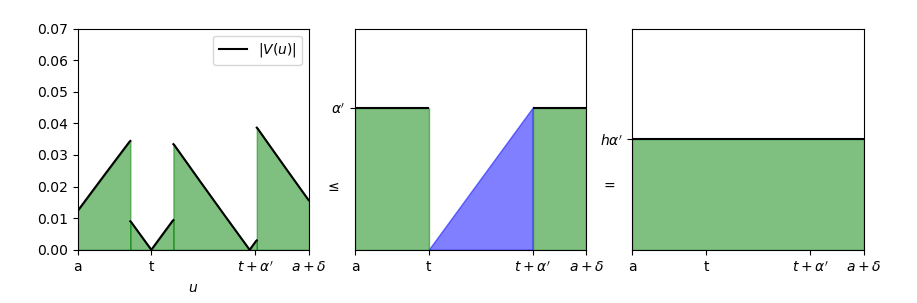
Osserviamo che h \alpha^{\prime} \lt \alpha^{\prime}, per cui questa maggiorazione è migliore di quella del limite superiore della formula (1): in quest’ultimo caso l’altezza del rettangolo sarebbe stata \alpha^{\prime}.
Intervalli in cui V non ha zeri
Ora, mantenendo la supposizione che \delta \geq \alpha^{\prime} \gt 0, analizziamo il caso complementare rispetto al precedente: supponiamo che V non abbia zeri in [a, a + \delta - \alpha^{\prime}]. Per poter confrontare meglio i due casi, anche ora scegliamo un punto t tale che [t, t + \alpha^{\prime}] \subseteq [a, a + \delta]. Chiaramente questa volta t non è uno zero di V, ma può essere un punto arbitrario. Scegliamo t in modo da far coincidere gli estremi destri degli intervalli [t, t + \alpha^{\prime}] e [a, a + \delta], quindi in modo che t + \alpha^{\prime} = a + \delta. In questo modo l’intervallo [a, a + \delta] risulta suddiviso in due parti (se non avessimo fatto coincidere gli estremi degli intervalli, le parti sarebbero state tre ed i calcoli sarebbero stati un po’ più lunghi):
Nell’intervallo [t, t + \alpha^{\prime}] possiamo applicare la maggiorazione mediante il limite superiore: sostituendo \delta := \alpha^{\prime} nella (1), si ottiene:
Nel caso precedente, quando t era uno zero, avevamo ottenuto un’approssimazione migliore tra t e t + \alpha^{\prime} (formula (4) con \epsilon := \alpha^{\prime}); in questo caso, però, possiamo in compenso migliorare la maggiorazione dell’integrale nell’intervallo [a, t]. Mentre prima per questo intervallo avevamo applicato la maggiorazione col limite superiore, ora possiamo ragionare diversamente, perché sappiamo che V non ha zeri in [a, t] (perché per ipotesi non ne ha in [a, a + \delta] e [a, t] \subseteq [a, a + \delta]). In particolare possiamo applicare il seguente Lemma:
In un intervallo, se V non ha zeri cambia segno al più una volta
Sia I un intervallo reale nel quale V non ha zeri. Allora V cambia segno al più una volta in I.
Ragionando per contraddizione, supponiamo che V cambi segno almeno due volte in I: dobbiamo dimostrare che V ha almeno uno zero in I, arrivando quindi a una contraddizione con l’ipotesi.
Se la funzione cambia segno almeno due volte, allora esistono quattro punti a, b, c, d \in I tali che a \lt b \lt c \lt d e si verifica una delle seguenti possibilità:
- caso 1: V \geq 0 in [a, b], V \leq 0 in [b, c], V \geq 0 in [c, d]
- caso 2: V \leq 0 in [a, b], V \geq 0 in [b, c], V \leq 0 in [c, d]
In entrambi i casi, esistono tre punti e, f, g \in I tali che e \lt f \lt g e V \geq 0 in [e, f], V \leq 0 in [f, g] (nel primo caso [e, f] = [a, b] e [f, g] = [b, c], nel secondo caso [e, f] = [b, c] e [f, g] = [c, d]). Ciò significa che la funzione V è continua in f. Vediamo perché. Se osserviamo il grafico della funzione (Figura 2 dell’articolo Le funzioni W e V), possiamo notare che i punti di discontinuità di V corrispondono a salti da valori più piccoli a valori più grandi, mai il viceversa. Per il momento prendiamo per buona questa proprietà, che dimostreremo tra poco. Di conseguenza possiamo dire che, se f fosse un punto di discontinuità di V, allora i valori assunti da V in un intorno destro di f sarebbero maggiori di quelli assunti in un intorno sinistro. Ma questo è in contrasto col fatto che V è positiva o nulla a sinistra di f e negativa o nulla a destra (casomai dovrebbe essere il contrario); quindi V deve essere continua in f.
Ora, per definizione di continuità, sia il limite destro che il limite sinistro di V(u) per u \to f esistono e sono uguali a V(f). Ma il limite sinistro deve essere maggiore o uguale a zero, perché V \geq 0 a sinistra di f; analogamente il limite destro deve essere minore o uguale di zero, perché anche V lo è a destra di f. Quindi l’unica possibilità, per la continuità di V in f, è che sia \lim_{u \to f}^+ V(u) = \lim_{u \to f}^- V(u) = 0 = V(f). Quindi V ammette uno zero in I (e questo zero è f).
Per completare la dimostrazione, resta da dimostrare la proprietà che abbiamo preso per buona basandoci sul grafico della funzione, ossia che i punti di discontinuità di V corrispondono a salti da valori più piccoli a valori più grandi. Questa proprietà si dimostra partendo dall’osservazione dopo la definizione di V, secondo cui per ogni u \in \mathbb{R}^+:
da cui
Chiaramente i punti di discontinuità di questa funzione discendono da quelli di \overline{\psi}, perché tutte le altre funzioni in gioco sono continue. Ma \psi è una funzione crescente, per cui lo è anche la sua estensione semplice \overline{\psi}. Quindi, se h è un punto di discontinuità di \overline{\psi}, essa in questo punto farà un salto da valori più piccoli a valori più grandi. Più formalmente, il valore assunto dalla funzione in h sarà maggiore di quelli assunti in un intorno sinistro di esso. Chiamando I_s questo intorno sinistro, esiste quindi una costante \delta \gt 0 tale che:
da cui
Ora, facendo tendere k ad h, a un certo punto i valori di \overline{\psi}(k) saranno costanti, perchè ci troveremo in uno dei tratti costanti dell’estensione semplice, prima del salto in h. Quindi per un intorno sinistro I_s^{\prime} \subseteq I_s e per una certa costante C, tenendo conto che k \leq h, avremo che:
Quindi, essendo \delta \gt 0:
da cui, per la (k), abbiamo che:
cioè la funzione, in \log h, fa un salto da valori più piccoli a valori più grandi. Ma, come abbiamo osservato prima, i punti di discontinuità di V discendono da quelli di \overline{\psi}: in particolare \log h è un punto di discontinuità di V se e solo se h è un punto di discontinuità di \overline{\psi}. Quindi il ragionamento che abbiamo fatto vale per tutti i punti di discontinuità di V.
Quindi possiamo essere certi che V cambia segno al più una volta nell’intervallo [a, t]. Allora esistono solo quattro possibilità:
- V è sempre positiva in [a, t]
- V è sempre negativa in [a, t]
- V è sempre positiva in [a, m] e sempre negativa in [m, t], dove m è tale che a \lt m \lt t
- V è sempre negativa in [a, m] e sempre positiva in [m, t], dove m è tale che a \lt m \lt t
Nei primi due casi, per la prima e la seconda idea dell’articolo precedente, in particolare per il Lemma N.14, possiamo maggiorare l’integrale di |V| come segue:
dove A è una certa costante positiva (di cui non ci serve conoscere il valore).
Negli altri due casi possiamo ripetere lo stesso ragionamento nei due intervalli [a, m] e [m, t], ottenendo:
Ma, essendo 2A \lt 4A, possiamo unire le due formule precedenti in un’unica formula che vale in tutti e quattro i casi:
Quindi, per le formule (6), (7) e (8), abbiamo che:
Ora chiediamoci: quest’approssimazione è buona? Cioè, è migliore della (1), che è quella che si otterrebbe mediante la maggiorazione del limite superiore? Se così fosse, dovrebbe valere la relazione:
Equivalentemente, esprimendoci nei termini del Lemma N.15, per i motivi spiegati nella dimostrazione dello stesso, possiamo dire che:
Ovviamente, fissato \delta, questa relazione può essere vera o falsa a seconda del valore di A, che però non conosciamo. Conviene, allora, ragionare al contrario: essendo il valore di A fisso, possiamo trovare un valore di \delta tale che la (10) sia vera. Così, per tutti gli intervalli di tale ampiezza, la maggiorazione (9) sarebbe migliore della (1). Otteniamo così il seguente Lemma:
Maggiorazione dell’integrale di |V| migliore di quella del limite superiore, secondo caso
Supponiamo che \alpha^{\prime} \gt 0. Sia A la costante del Lemma N.14, siano \delta \geq \alpha^{\prime} e a \geq 0. Se nell’intervallo [a, a + \delta - \alpha^{\prime}] la funzione |V| non ha zeri, e se inoltre esiste una costante k \lt 1 tale che
allora:
Calcolo dell’ampiezza dell’intervallo
Finora abbiamo trovato due modi per ottenere una maggiorazione dell’integrale di |V| nell’intervallo [a, a + \delta]: prima nel caso in cui V ha almeno uno zero nell’intervallo, poi nel caso in cui non ha zeri. In entrambi i casi abbiamo trovato un’approssimazione migliore di quella del limite superiore. Il problema è che in ciascun caso abbiamo posto dei vincoli su \delta. Se vogliamo fare un discorso generale, dobbiamo assicurarci che esista un valore di \delta che soddisfa i vincoli di entrambi i casi: così facendo, fissato qualsiasi intervallo di ampiezza \delta, saremmo certi che valga sempre una maggiorazione migliore di quella del limite superiore, sia che si verifichi il primo caso, sia che si verifichi il secondo.
Innanzitutto, in entrambi i casi precedenti abbiamo supposto che \delta \geq \alpha^{\prime}. In ciascun caso abbiamo fatto inoltre un’ipotesi aggiuntiva diversa:
- Nel primo caso abbiamo supposto che esiste una costante h \lt 1 tale che (\delta - \alpha^{\prime}) \alpha^{\prime} + \frac{(\alpha^{\prime})^2}{2} = \delta h \alpha^{\prime}
- Nel secondo caso abbiamo supposto che esiste una costante k \lt 1 tale che 4A + (\alpha^{\prime})^2 = \delta k \alpha^{\prime}
Quindi possiamo dire che un numero \delta soddisfa le ipotesi di entrambi i casi, cioè sia del Lemma N.15 che del Lemma N.17, se è soluzione del sistema:
Con un po’ di calcoli algebrici, si ottiene la seguente tipologia di soluzioni (ve ne sono anche altre, ma non ci interessa trovarle tutte):
Dato che non ci serve trovare tutte le soluzioni, ma basta trovarne anche una sola, possiamo supporre che sia k \leq h. Vedremo quindi quali soluzioni ci sono in questo caso e trascureremo quelle che si possono ottenere quando k \gt h:
A questo punto la penultima condizione diventa superflua, essendo conseguenza delle due precedenti (se k \leq h e h \lt 1, anche k \lt 1):
Se ora applichiamo l’ultima disequazione al secondo membro della seconda, otteniamo \alpha^{\prime} k \delta \leq \alpha^{\prime} h \delta; ma così facendo l’ultima disequazione stessa diventa ridondante, perché si può ricavare appunto da \alpha^{\prime} k \delta \leq \alpha^{\prime} h \delta:
La seconda riga ora è contemporaneamente un’equazione e una disequazione. Separiamo parte dell’equazione ricavando k:
Così ci siamo liberati di k e possiamo concentrarci sulle altre due variabili, h e \delta.
Dividendo la prima equazione per \alpha^{\prime}, si ottiene (\delta - \alpha^{\prime}) + \frac{\alpha^{\prime}}{2} = h \delta, da cui \delta - \frac{\alpha^{\prime}}{2} = h \delta e h = 1 - \frac{\alpha^{\prime}}{2 \delta} (quest’ultimo passaggio presuppone che \delta \neq 0, ma questa supposizione è lecita, perché una delle disequazioni del sistema è \delta \geq \alpha^{\prime} e per ipotesi \alpha^{\prime} \gt 0). Questo valore di h rende superflua la quarta condizione, perché, essendo \delta \geq \alpha^{\prime} \gt 0, 1 - \frac{\alpha^{\prime}}{2 \delta} \lt 1. Otteniamo quindi:
Sostituendo il valore di h nella seconda formula del sistema, si ottiene 4A + (\alpha^{\prime})^2 \leq \alpha^{\prime} \left( 1 - \frac{\alpha^{\prime}}{2 \delta} \right) \delta, da cui 4A + (\alpha^{\prime})^2 \leq \alpha^{\prime} \delta - \frac{(\alpha^{\prime})^2}{2} \Rightarrow 4A + \frac{3 (\alpha^{\prime})^2}{2} \leq \alpha^{\prime} \delta \Rightarrow \delta \geq \frac{4A}{\alpha^{\prime}} + \frac{3 \alpha^{\prime}}{2}. Chiaramente questo valore è maggiore di \alpha^{\prime}, quindi la terza condizione è superflua. Otteniamo così la soluzione finale:
Quindi basta fissare un valore di \delta maggiore o uguale di \frac{4A}{\alpha^{\prime}} + \frac{3 \alpha^{\prime}}{2} e sostituirlo nelle equazioni della (11), per ottenere i corrispondenti valori di h e k e quindi una particolare soluzione del sistema. Per tale soluzione valgono allora le ipotesi sia del Lemma N.15 che del Lemma N.17, quindi:
per cui, essendo k \leq h:
Riassumendo, possiamo enunciare la seguente Proposizione:
Maggiorazione dell’integrale di |V| migliore di quella del limite superiore, in intervalli di ampiezza opportuna
Supponiamo che \alpha^{\prime} \gt 0. Sia \delta \geq \frac{4A}{\alpha^{\prime}} + \frac{3 \alpha^{\prime}}{2}, dove A è la costante del Lemma N.14. Allora esiste una costante h \lt 1 tale che, per ogni a \geq 0:
Fine della dimostrazione
Torniamo ora all’intervallo di partenza [0, \log \xi]. Osserviamo che, se \log \xi \geq \frac{4A}{\alpha^{\prime}} + \frac{3 \alpha^{\prime}}{2}, potremmo applicare direttamente la Proposizione N.27 con \delta := \log \xi e a := 0. Quindi, supponendo che \alpha^{\prime} \gt 0, esiste h \lt 1 tale che:
da cui, essendo \log \xi \gt 0 e per il Corollario 1 della Proprietà A.8:
Ora passiamo al limite superiore:
La (12) non vale per ogni \xi ma, come abbiamo supposto inizialmente, vale solo se \log \xi \geq \frac{4A}{\alpha^{\prime}} + \frac{3 \alpha^{\prime}}{2}. Tuttavia, non ci interessa cosa accade per valori di \log \xi più piccoli di \frac{4A}{\alpha^{\prime}} + \frac{3 \alpha^{\prime}}{2}, perché vogliamo sapere cosa accade per \xi \to +\infty: il limite superiore (come alche il limite) per \xi \to +\infty non è influenzato dal comportamento delle funzioni in gioco per valori di \xi più piccoli di un valore prefissato. Quindi la formula (13) è sempre verificata, perché \xi ha cambiato significato dalla (12) alla (13): da essere un numero reale prefissato, è diventato la variabile del limite superiore.
Il membro di sinistra della (13) è per definizione pari a \beta^{\prime} (v. Definizione N.23), mentre il membro di destra è uguale a h \alpha^{\prime} (perché h e \alpha^{\prime} non dipendono da \xi, mentre o\left( \frac{1}{\log \xi} \right) tende a zero). Quindi:
Ma, essendo h \lt 1:
Questa relazione, però, è in contrasto con la Proposizione N.26. Quindi la nostra assunzione che \alpha^{\prime} \gt 0, l’unica assunzione arbitraria che a questo punto ci è rimasta, deve essere errata. Ricordando che \alpha^{\prime} \geq 0, possiamo dire allora che:
Per il Lemma N.7, quest’equazione è una condizione sufficiente perché sia vero il Teorema dei numeri primi, quindi la dimostrazione è conclusa.