Prerequisiti:
- Fine della prima parte della dimostrazione: la relazione tra \alpha e \beta^{\prime}
- Il Teorema di Selberg: dimostrazione e applicazione
- Le funzioni W e V
- Proprietà degli ordini asintotici
- Il limite inferiore e il limite superiore di una successione
- Elementi di analisi asintotica
In questo articolo vedremo quali sono le idee su cui si basa la seconda parte della dimostrazione del Teorema dei numeri primi. Finora abbiamo dimostrato che \alpha \leq \beta^{\prime}, dove \alpha e \beta^{\prime} sono due costanti importanti legate alla funzione V. Come abbiamo visto, se dimostrassimo che \alpha = 0 avremmo dimostrato il Teorema dei numeri primi. Per dimostrarlo, una prima idea potrebbe essere dimostrare che \beta^{\prime} = 0, perché così si avrebbe che \alpha \leq \beta^{\prime} = 0, da cui \alpha = 0. In questo articolo tenteremo di dimostrare che \beta^{\prime} = 0 (e vedremo perché per il momento resterà solo un tentativo).
Per prima cosa, ricordiamo la definizione di \beta^{\prime}:
Vogliamo quindi dimostrare che:
Per il momento, lasciamo stare il limite superiore e cerchiamo di andare al nòcciolo della questione: la funzione di cui si calcola il limite superiore sicuramente deve diventare molto piccola al crescere di \xi; altrimenti il limite superiore non potrebbe essere zero. Ma che significa “molto piccola”? Per precisare meglio quest’espressione, possiamo fissare un certo numero reale \epsilon \gt 0 che riteniamo essere molto piccolo: così “molto piccolo” significa “minore di \epsilon“.
Quindi, tenteremo di dimostrare che:
dove \epsilon \gt 0 è un numero reale positivo fissato a priori, che dovrebbe essere più piccolo possibile. Quest’ultima disuguaglianza può essere riscritta come segue:
Questo semplice passaggio algebrico è molto importante dal punto di vista concettuale, perché ci permette di vedere il problema in termini geometrici: infatti, la (3) significa che l’area compresa tra il grafico della funzione |V| e l’asse orizzontale, tra 0 e \log \xi, è minore di \epsilon \log \xi.
Ma la quantità \epsilon \log \xi a sua volta è interpretabile come un’area: corrisponde infatti all’area di un rettangolo avente per base \log \xi e per altezza \epsilon. La formula (3) rappresenta quindi un confronto tra l’area sottesa al grafico della funzione |V| e l’area di un rettangolo:
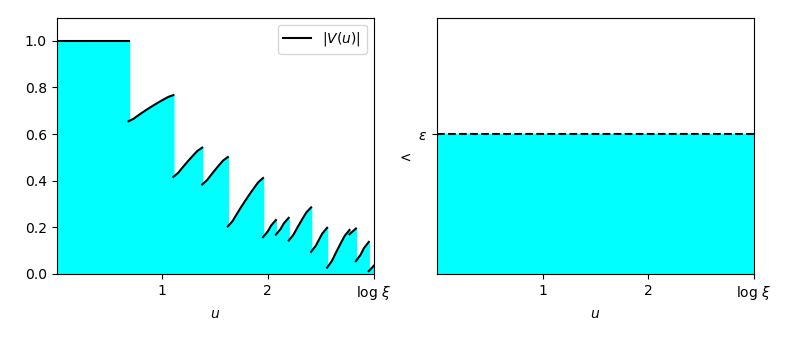
Come rendere quindi l’area a sinistra più piccola di quella a destra, tenendo conto del fatto che \epsilon dovrebbe essere più piccolo possibile? Per rispondere a questa domanda, illustreremo quattro idee principali.
Prima idea: partire da una maggiorazione col valore assoluto fuori dall’integrale
Per cominciare, osserviamo che le cose si fanno molto più semplici se si porta il valore assoluto fuori dall’integrale. Infatti, si può dimostrare la seguente Proposizione:
Maggiorazione del valore assoluto dell’integrale di V tra 0 e un numero positivo
Esiste un numero reale A \gt 0 tale che, per ogni \xi \gt 0:
Nell’articolo Le funzioni W e V, abbiamo già dimostrato la seguente formula (numerata (4′) nell’articolo citato):
In realtà, riguardando come è stata dimostrata, si può notare come lo stesso ragionamento valga anche considerando un valore reale positivo \xi al posto dell’intero x:
Per la Definizione A.3, quest’ultima uguaglianza asintotica significa che esiste una costante positiva B tale che \left| \int_0^{\log \xi} V(u)\ du \right| \lt B definitivamente, cioè per ogni \xi maggiore o uguale a un certo \xi_0. Quindi, per dimostrare la Proposizione N.24, dobbiamo dimostrare che anche per \xi \lt \xi_0 vale una relazione simile.
Per la Proposizione N.7A, la funzione |V| è limitata, cioè esiste una costante C tale che V(u) \leq C per ogni u. Allora \left| \int_0^{\log \xi} V(u)\ du \right| \leq \left| \int_0^{\log \xi} C\ du \right| \leq \left| C \log \xi \right| = |C| \log \xi. Quindi, essendo il logaritmo crescente, per \xi \lt \xi_0 si ha che \left| \int_0^{\log \xi} V(u)\ du \right| \leq |C| \log \xi \lt |C| \log \xi_0.
In definitiva, considerando sia il caso \xi \geq \xi_0 che il caso \xi \lt \xi_0, abbiamo che \left| \int_0^{\log \xi} V(u)\ du \right| \lt \max(B, |C| \log \xi_0). A questo punto la Proposizione N.24 si ottiene ponendo A := \max(B, |C| \log \xi_0).
Il problema di questa Proposizione è che il valore assoluto si trova fuori dall’integrale e non dentro. In pratica, l’integrale qui calcola le aree comprese tra il grafico della funzione V e l’asse orizzontale col segno, ossia quelle sopra l’asse orizzontale col segno positivo, e quelle sotto di esso col segno negativo:
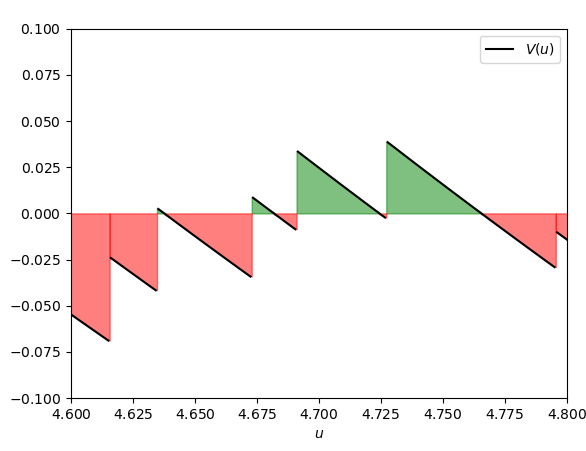
Quindi, l’integrale \int_0^{\log \xi} V(u)\ du è dato dal risultato della sottrazione delle aree negative da quelle positive. Perciò, l’unico effetto del valore assoluto nella Proposizione N.24 è che, se il risultato di quest’operazione risultasse negativo (come nella figura sopra, in cui le aree negative sono visibilmente più estese di quelle positive), il valore assoluto lo porterebbe ad essere un numero positivo.
Se invece il valore assoluto si trovasse all’interno dell’integrale, l’effetto sarebbe che le aree negative risulterebbero ribaltate, perciò sarebbero considerate come delle aree positive:
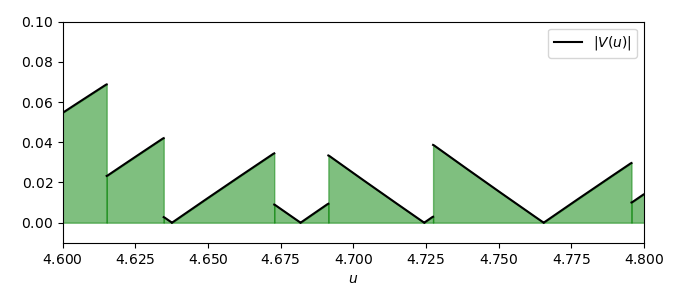
È evidente che in quest’ultimo caso l’area finale è maggiore rispetto a prima, perché ora tutte le aree hanno segno positivo. Questo spiega la difficoltà di utilizzare la Proposizione N.24 per dimostrare la (3): anche se riuscissimo a dimostrare che \left| \int_0^{\log \xi} V(u)\ du \right| \lt \epsilon \log \xi, l’espressione che interessa a noi, \int_0^{\log \xi} |V(u)|\ du, potrebbe essere maggiore di \left| \int_0^{\log \xi} V(u)\ du \right| e quindi anche maggiore di \epsilon \log \xi, vanificando il nostro sforzo.
Esiste però un caso particolare in cui la Proposizione N.24 può essere davvero utile: possiamo utilizzarla finché la funzione V non cambia segno. In effetti, come si può vedere nella Figura 2 dell’articolo Le funzioni W e V, inizialmente la funzione V è sempre negativa, per cui se il nostro \xi non è troppo grande abbiamo che:
Supponiamo che \xi sia abbastanza piccolo perché V sia sempre negativa tra 0 e \log \xi. Allora:
Ma l’integrale \int_0^{\log \xi} V(u)\ du non può essere positivo, perché V è negativa in tutto l’intervallo di integrazione, quindi:
Unendo le due formule precedenti, si ottiene la (4).
e quindi, per la Proposizione N.24:
Se vale questa relazione, allora vale anche la (3), a patto che sia
Ma A ed \epsilon sono fissi, mentre \xi è variabile, perciò A può essere reso minore di \epsilon \log \xi scegliendo un valore di \xi opportunamente grande. Bisogna però approfondire ulteriormente, perché non è detto che fino a questo \xi opportunamente grande la funzione V sia sempre negativa, come richiederebbe la formula (4) da cui siamo partiti.
Seconda idea: suddividere in intervalli più piccoli
A questo punto ci viene in aiuto la seconda idea. Se suddividiamo l’intervallo [0, \log \xi] in intervalli più piccoli, possiamo studiare ciascuno di questi intervalli separatamente, col vantaggio che possiamo scegliere gli estremi degli intervalli a nostro piacimento; l’unico vincolo è che il primo intervallo deve cominciare con 0 e l’ultimo deve finire con \log \xi.
In generale, quindi, possiamo supporre di avere una sequenza di intervalli del tipo [0, t_1], [t_1, t_2], [t_2, t_3], \ldots, [t_n, \log \xi], con 0 \lt t_1 \lt t_2 \lt t_3 \lt \ldots \lt \log \xi, dove t_1, t_2, t_3, \ldots, t_n sono dei punti opportuni, a nostra scelta, dell’intervallo [0, \log \xi] (ed anche n è a nostra scelta). In ciascuno di questi intervalli possiamo applicare il seguente Corollario della Proposizione N.24:
Maggiorazione del valore assoluto dell’integrale di V tra due numeri positivi o nulli
Esiste un numero reale A \gt 0 tale che, per ogni a \geq 0 e per ogni b \gt a:
Se a = 0, basta applicare la Proposizione N.24 facendo in modo che \log \xi = b, ossia ponendo \xi := e^{b}.
Se invece a \gt 0, abbiamo che:
dove nell’ultima disuguaglianza abbiamo applicato la Proposizione N.24.
Abbiamo voluto enfatizzare il fatto che la costante A che compare in questo Corollario è la stessa della Proposizione N.24, utilizzando lo stesso simbolo. In alternativa, avremmo potuto porre B := 2A ed enunciare il Corollario come segue:
Esiste un numero reale B \gt 0 tale che, per ogni a \geq 0 e per ogni b \gt a:
Questo Corollario supera le limitazioni della Proposizione N.24 perché, mentre prima dovevamo supporre che la funzione V sia sempre negativa tra 0 e \xi, ora siamo noi a scegliere gli intervalli, per cui possiamo scegliere qualsiasi intervallo in cui la funzione V è sempre negativa. Se [a, b] è un tale intervallo, con una dimostrazione analoga a quella della (4) abbiamo che:
per cui
Non solo: possiamo anche trattare il caso opposto. Infatti, le formule (4′) e (5′) continuano a valere anche se scegliamo un intervallo [a, b] in cui V è sempre positiva.
Perché le formule (4′) e (5′) valgono anche se V è sempre positiva nell’intervallo [a, b]?
In questo caso la dimostrazione è più semplice di quella per il caso negativo, perché, se nell’intervallo [a, b] la funzione V è sempre positiva, allora nell’integrale \int_{a}^{b} |V(u)|\ du si ha che |V(u)| = V(u), per cui l’integrale stesso è uguale a \int_{a}^{b} V(u)\ du ed assume un valore non negativo, in quanto \forall u \in [a, b]: V(u) \gt 0 \Rightarrow \int_{a}^{b} V(u)\ du \geq \int_{a}^{b} 0\ du = 0. Allora entrambi gli integrali \int_{a}^{b} |V(u)|\ du e \int_{a}^{b} V(u)\ du coincidono col proprio valore assoluto, perciò \int_{a}^{b} |V(u)|\ du = \int_{a}^{b} V(u)\ du = \left| \int_{a}^{b} V(u)\ du \right|.
Possiamo quindi enunciare il seguente Lemma:
Maggiorazione dell’integrale di V negli intervalli in cui non cambia segno
Sia [a, b] un intervallo in cui la funzione V è sempre positiva o sempre negativa. Allora esiste una costante positiva A tale che:
Portando all’estremo questo procedimento, qualunque sia \xi potremmo suddividere l’intervallo [0, \xi] in tutti e soli i sotto-intervalli in cui la funzione è sempre positiva o sempre negativa, cambiando intervallo appena la funzione cambia segno.
Osservando il grafico della funzione V (v. Figura 2), possiamo notare che esso è formato da un susseguirsi di tratti continui e decrescenti. Ci sono quindi solo due modi in cui la funzione può cambiare segno man mano che ci si sposta verso destra:
- Un tratto continuo e decrescente attraversa l’asse orizzontale in un punto t: in questo caso t sarà l’estremo superiore di un intervallo e l’estremo inferiore di quello successivo.
- Un tratto continuo e decrescente in cui la funzione è negativa è seguito da un tratto continuo e decrescente in cui la funzione è positiva, e tra i due vi è una discontinuità in un punto t, appartenente ad uno dei due tratti: anche in questo caso t sarà l’estremo superiore di un intervallo e l’estremo inferiore di quello successivo.
Quindi, la costruzione funziona in questo modo:
- si individuano i punti in cui la funzione V assume valore 0 o ha una discontinuità;
- si spezza l’intervallo [0, \log \xi] in corrispondenza di tali punti, ottenendo una sequenza di intervalli del tipo [0, t_1], [t_1, t_2], [t_2, t_3], \ldots, [t_n, \log \xi].
Dato che in ciascun intervallo così individuato la funzione ha sempre lo stesso segno, ponendo t_0 := 0 e t_{n+1} := \xi, per la (5′) avremmo che:
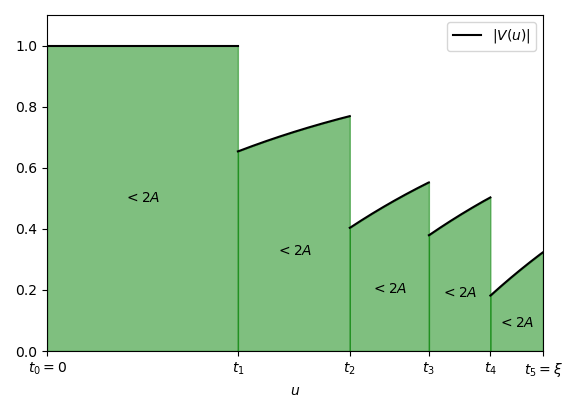
Ora supponiamo che l’ampiezza dell’i-esimo intervallo, t_{i+1} - t_i, sia abbastanza grande perché sia 2A \lt \epsilon (t_{i+1} - t_i), dove \epsilon è la costante che abbiamo fissato inizialmente. Allora avremmo che:
A questo punto, sommando per tutti gli indici i, ed osservando che la somma di tutte le ampiezze è \log \xi, avremmo che:
Si potrebbe così dimostrare la (3). Il problema è che l’ipotesi 2A \lt \epsilon (t_{i+1} - t_i) certamente non può essere rispettata per valori di \epsilon piccoli a piacimento: più è piccolo \epsilon, più dovrebbe essere grande t_{i+1} - t_i; ma questa quantità non può essere grande a piacimento, perché è fissa, essendo determinata da dove sono collocati gli zeri e i punti di discontinuità di V. La prossima idea può aiutarci a superare questo problema.
Terza idea: studiare come cresce il valore assoluto di V dopo uno zero
L’idea precedente prevedeva di suddividere l’intervallo [0, \log \xi] nei sottointervalli [0, t_1], [t_1, t_2], [t_2, t_3], \ldots, [t_n, \log \xi], in modo che, per i = 1,\ldots,n, t_i sia un punto di discontinuità di V oppure uno zero di V. Ora concentriamoci su quest’ultimo caso: se V(t_i) = 0, cosa succede in un intorno di t_i? Può darsi che la funzione V, per punti vicini a t_i, assuma valori vicini a zero, o comunque limitabili in qualche modo. Per esempio, supponiamo di riuscire a trovare qualche funzione che limita la crescita di |V| nell’intorno di un suo zero, ossia una funzione positiva f tale che, per ogni h \geq 0, |V(t_i + h)| \leq f(h):
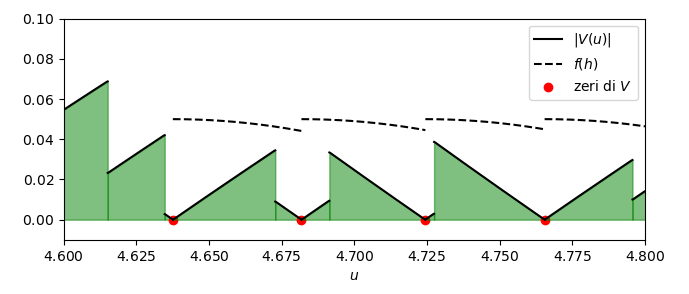
Allora:
A questo punto, se la funzione f nell’intervallo [t_i, t_{i+1}] fosse sempre minore o uguale di \epsilon, avremmo che:
Avremmo ottenuto quindi lo stesso risultato della (6), ma procedendo per un’altra via. Il vantaggio in questo caso è che, una volta trovato uno zero di V, in un suo intorno non facciamo ipotesi di nessun genere su V; prima invece ci serviva che essa avesse segno costante, pertanto eravamo costretti a scegliere gli estremi degli intervalli in un certo modo.
Effettivamente è possibile ragionare nel modo descritto, grazie alla seguente Proposizione:
Maggiorazione del valore assoluto di V dopo un suo zero
Sia t uno zero di V. Allora, per ogni h \geq 0:
Per ipotesi, V(t) = R(e^t) = 0. Possiamo quindi riscrivere il numero |V(t + h)| come segue:
Così facendo, al numeratore abbiamo ottenuto due termini del tipo R(\xi) \log \xi, con \xi \gt 0, che ricorda il primo termine del Teorema di Selberg. Infatti, se in questo Teorema consideriamo la variabile reale \xi al posto della variabile intera x, otteniamo questo enunciato:
Nell’articolo Il Teorema di Selberg: dimostrazione e applicazione, in particolare nella formula (5), abbiamo visto che \sum_{n \leq x} \Lambda(n) R\left( \frac{x}{n} \right) = \sum_{nm \leq x} \Lambda(n) \Lambda(m) - x \log x + O(x). Mantenendo la convenzione che \sum_{n \leq \xi} := \sum_{n \leq \left \lfloor \xi \right \rfloor}, possiamo sostituire quest’uguaglianza nella (b):
da cui, applicando il Corollario della Proprietà A.9, si ottiene:
Ora, sostituendo prima \xi := e^{t + h} e poi \xi := e^t, e infine sottraendo membro a membro, si ottiene:
Ma la sommatoria non può essere negativa, perché \Lambda è una funzione non negativa, quindi:
Essendo h costante ed applicando in sequenza le Proprietà A.5, Corollario della Proprietà A.7, A.16, A.10, Corollario della Proprietà A.9 e A.11, O(t + h) = O(O(t) + O(1)) = O(O(t) + o(t)) = O(O(t) + O(t)) = O(O(t)) = O(t). Sostituendo, ed applicando le Proprietà Corollario 3 della Proprietà A.8 e Corollario della Proprietà A.9, si ottiene infine:
Sostituendo nella (a), si ottiene:
Il secondo termine dentro il valore assoluto si può sviluppare come segue:
dove il passaggio (*) si giustifica osservando che \left| \frac{h}{t + h} \right| = \frac{h}{t + h} \leq \frac{h}{t}, per cui, in base alla Definizione A.3, \frac{h}{t + h} = O\left( \frac{1}{t} \right); inoltre nel passaggio finale abbiamo applicato il Corollario 3 della Proprietà A.8.
Per quanto riguarda il terzo termine dentro il valore assoluto della (c), abbiamo che:
dove:
- Nel primo passaggio abbiamo applicato il Corollario I della Proprietà A.8.
- Il passaggio centrale è dovuto al fatto che \lim_{t \to +\infty} \frac{t}{e^{t+h}(t + h)} / \frac{1}{t} = \lim_{t \to +\infty} \frac{t^2}{e^{t+h}(t + h)} = 0 perché nella frazione \frac{t^2}{e^{t+h}(t + h)} vi è al numeratore un infinito di ordine 2, mentre al denominatore vi è un infinito di ordine infinitamente grande (funzione esponenziale); quindi, per la Definizione A.4, \frac{t}{e^{t+h}(t + h)} = o\left( \frac{1}{t}\right).
- Nel passaggio seguente abbiamo applicato le Proprietà A.16 e A.10.
Sostituendo la (d) e la (e) nella (c), ed applicando il Corollario della Proprietà A.9, si ottiene:
da cui
dove nell’ultimo passaggio abbiamo applicato la Proprietà A.6 ed abbiamo osservato che, essendo h \geq 0, si ha che e^h \geq 1 \Rightarrow \frac{1}{e^h} \leq 1 \Rightarrow 1 - \frac{1}{e^h} \geq 0.
La funzione f in questo caso è f(h) = 1 - \frac{1}{e^h}, con un errore di O\left(\frac{1}{t}\right) (questo errore quindi tende a zero se t tende a infinito).
Quarta idea: se \epsilon \geq \alpha^{\prime}, si può ampliare un intervallo a piacimento
Le idee precedenti erano importanti, ma quella che presentiamo adesso farà veramente la differenza. Supponiamo che, con uno dei metodi precedenti, si sia riusciti a trovare un intervallo [a, b] \subseteq [0, \log \xi] tale che:
Sia nella prima che nella seconda idea, però, l’intervallo [a, b] doveva essere opportunamente grande perché valga una relazione di questo tipo, ma allo stesso tempo non poteva essere grande a piacimento, essendo vincolato dagli zeri e dai punti di discontinuità di V. Se però ammettiamo che \epsilon \geq \alpha^{\prime}, esiste un modo molto semplice per maggiorare l’integrale di |V| in un intervallo più grande di [a, b], diciamo [A, B], con A \leq a \lt b \leq B, sempre contenuto in [0, \log \xi]. Questo metodo consiste nello spezzare l’intervallo [A, B] in tre parti:
Nella prima e nell’ultima parte possiamo maggiorare l’integrale di |V| utilizzando una conseguenza della definizione di \alpha^{\prime}. Essendo \alpha^{\prime} il limite superiore della funzione |V|, per la Proprietà A.18 quest’ultima è maggiorata in tutto il suo dominio da \alpha^{\prime} a meno di un errore infinitesimo, ossia:
Dato che questa relazione vale per ogni u \in [0, +\infty), a maggior ragione vale anche per ogni u \in [A, a] e per ogni u \in [b, B], per cui:
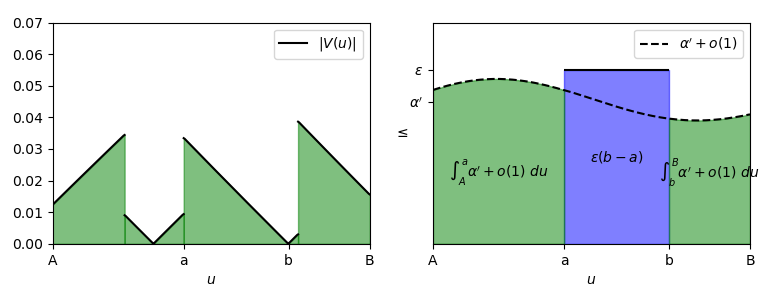
Quindi, per la (7) e la (8):
Semplificando, la prima disuguaglianza della (8) diventa:
Ora dimostriamo che \int_A^a o(1)\ du = o(1). Per la Definizione A.4, il simbolo o(1) rappresenta una funzione che tende a zero. Quindi dobbiamo dimostrare che l’intero integrale \int_A^a o(1)\ du tende a zero. Ma tende a zero rispetto a cosa? Ricordiamo che la variabile delle notazioni asintotiche che compaiono nelle nostre formule è sempre \xi, l’estremo superiore dell’intervallo [0, \xi] che stiamo considerando, quindi il limite va calcolato sempre per \xi \to \infty. Tuttavia in questo caso non abbiamo un’espressione che coinvolge esplicitamente \xi, ma abbiamo A ed a; dobbiamo ricordare però che [A, a] \subseteq [A, B] \subseteq [0, \log \xi], per cui, se \xi tende a infinito, anche A ed a possono tendere a infinito. Tuttavia A ed a non sono variabili libere, ma vincolate dalla relazione A \leq a, per cui basta far tendere ad infinito A e porre a := A + h, dove h rappresenta l’ampiezza dell’intervallo, che è costante perché stabilita a priori. Quindi il significato dell’uguaglianza
è:
Ora che abbiamo chiarito ciò, possiamo passare alla dimostrazione vera e propria. Per definizione di limite, si tratta di dimostrare che, per ogni \lambda \gt 0, \left| \int_A^{A + h} o(1)\ du \right| \lt \lambda per A sufficientemente grande. A questo punto possiamo osservare che la funzione integranda o(1) tende a zero (rispetto a \xi, quindi anche rispetto ad A), quindi per ogni \tau \gt 0 si ha che |o(1)| \lt \tau per A sufficientemente grande. Allora, per A sufficientemente grande:
e questa quantità può essere resa minore di \lambda ponendo \tau \lt \frac{\lambda}{h}, concludendo la dimostrazione.
Per la seconda disuguaglianza della (8) si può fare un ragionamento analogo, dimostrando che \int_b^B o(1)\ du = o(1). Infine, nell’ultimo passaggio della (9) si è applicata la proprietà che la somma di due infinitesimi (o(1)) è ancora un infinitesimo.
Se ora supponiamo che \epsilon \geq \alpha^{\prime}, per la (9) abbiamo che:
Praticamente, partendo dalla (7), abbiamo maggiorato l’integrale su un intervallo più ampio di quello di partenza, commettendo un errore infinitesimo.
Cambio di strategia: porre \epsilon := \alpha^{\prime}
L’ultima idea può far cadere il discorso iniziale, perché \epsilon dovrebbe essere più piccolo possibile, mentre alla fine abbiamo supposto che sia maggiore o uguale di \alpha^{\prime}, che è una costante che a priori non sappiamo quanto vale. Posto che \alpha^{\prime} non può essere negativo, perché è definito come il limite superiore di una funzione non negativa, possiamo distinguere due casi:
- Se \alpha^{\prime} = 0 non ci sono problemi, perché il fatto che \epsilon \geq \alpha^{\prime} = 0 non impedisce che \epsilon sia piccolo quanto si vuole;
- Se \alpha^{\prime} \gt 0, la condizione \epsilon \geq \alpha^{\prime} è in contraddizione col fatto che \epsilon sia arbitrariamente piccolo, perché chiaramente \epsilon non potrebbe assumere tutti i valori compresi tra 0 e \alpha^{\prime}.
Nel secondo caso, però, possiamo cambiare la nostra strategia per raggiungere comunque il nostro scopo finale, ossia dimostrare che \alpha = 0. Infatti, possiamo ragionare in questo modo:
- Abbiamo già dimostrato, nel precedente articolo, che \alpha \leq \beta^{\prime};
- Modificando la dimostrazione, si potrebbe dimostrare che anche \alpha^{\prime} \leq \beta^{\prime};
- Se \alpha^{\prime} \gt 0, possiamo porre \epsilon := \alpha^{\prime} (operazione lecita in quanto \epsilon deve essere positivo e \alpha^{\prime} è un numero reale);
- Così facendo, con le stesse tecniche che ci consentirebbero di dimostrare che \beta^{\prime} \lt \epsilon, potremmo dimostrare che \beta^{\prime} \lt \alpha^{\prime};
- I punti 2 e 4, una volta dimostrati, sarebbero in contraddizione tra loro, perciò l’ipotesi \alpha^{\prime} \gt 0 non può essere vera: deve essere \alpha^{\prime} = 0;
- Se \alpha^{\prime} = 0, per la Proprietà N.24 anche \alpha = 0, per cui, per il Lemma N.7, il Teorema dei numeri primi sarebbe dimostrato.
Quindi gli unici punti aperti per concludere la dimostrazione sono il 2 e il 4.
Il punto 2 si risolverebbe interpretando x, nell’articolo precedente, come un numero reale invece che un numero intero. Molte volte, durante questo percorso, abbiamo visto che il passaggio dai numeri interi ai numeri reali è complicato; in questo caso però i cambiamenti da fare sono minimi. Basta, infatti, rivedere il Teorema di Selberg: come abbiamo osservato nella dimostrazione della Proposizione N.8, questo Teorema vale anche con x reale, e la dimostrazione resta sostanzialmente la stessa: è sufficiente interpretare le sommatorie del tipo \sum_{n \leq x}, con x reale, come \sum_{n \leq \lfloor x \rfloor} (in realtà, se x è reale, la sommatoria \sum_{n \leq x} è proprio definita come \sum_{n \leq \lfloor x \rfloor}). La dimostrazione della disuguaglianza \alpha^{\prime} \leq \beta^{\prime} non presenta quindi nessuna sostanziale novità; la sua utilità sarebbe più che altro quella di ripassare le dimostrazioni precedenti. Ci limiteremo quindi ad enunciare la seguente Proposizione, lasciandone la dimostrazione agli studenti più volenterosi:
Relazione tra \alpha^{\prime} e \beta^{\prime}
Con riferimento alla Definizione N.23:
Il punto 4 invece richiede maggiori dettagli: si tratta di mettere insieme le idee presentate in questo articolo per dimostrare che, se \alpha^{\prime} \gt 0, \beta^{\prime} \lt \alpha^{\prime}. Questo sarà l’argomento del prossimo articolo.