Studiando teoria dei numeri ci si accorge ben presto che occorre una certa dimestichezza con certi formalismi. In particolare, alcuni tipi di sommatorie sono di uso così comune che conviene trattarli separatamente, prima di applicarli in vari contesti. Questo è ciò che faremo in questo articolo, che in prima battuta può essere saltato, ma sarà un riferimento per gli articoli successivi.
Un po’ di formalismi sulle sommatorie
Sappiamo che, quando si devono sommare molti numeri, si può scrivere la somma in modo compatto utilizzando il simbolo di sommatoria. Ad esempio, la somma dei quadrati degli interi da 1 a n, dove n \geq 1 è un intero, si può scrivere come segue:
oppure, in modo equivalente:
o ancora:
Tutte le scritture precedenti sono equivalenti alla seguente scrittura per esteso:
Sebbene quest’ultimo tipo di notazione risulti spesso più comprensibile rispetto alle sommatorie equivalenti, spesso queste ultime risultano più comode quando si devono fare calcoli algebrici, in particolare nelle dimostrazioni.
In generale i termini di una sommatoria, cioè gli addendi della somma, possono essere il risultato di qualunque funzione f della variabile i, che è detto indice (o variabile) della sommatoria:
Calcolare questa sommatoria significa calcolare f(i) per ogni i = 1, \ldots, n, e sommare tutti i valori ottenuti: una corrispondente notazione estesa sarebbe f(1) + \ldots + f(n). È anche possibile, nella notazione estesa, esplicitare più termini prima dei puntini, ad esempio f(1) + f(2) + f(3) + \ldots + f(n); comunque, qualunque sia il numero di termini resi espliciti, si suppone che n sia almeno pari all’indice del primo termine, in questo caso 1, per cui se ad esempio n = 2 la notazione f(1) + f(2) + f(3) + \ldots + f(n) si riduce a f(1) + f(2): il termine f(3) non è realmente presente ma serve solo a far capire come si comporterebbe la sommatoria per valori di n più grandi.
In molte sommatorie utilizzate in teoria dei numeri, l’indice non varia tra tutti gli interi compresi tra 1 ed n, ma solamente tra i divisori di n, perciò di solito viene indicato con la variabile d:
Ciò significa calcolare f(d) solo per gli interi positivi d che dividono n, e sommare i valori ottenuti:
Sommatorie estese ai divisori di un numero intero positivo
Sia n \in \mathbb{N}^{\star}. Si definisce il seguente simbolo:
dove per “divisori” si intendono, come di consueto, i divisori positivi.
Per chiarire la differenza tra la sommatoria (1) e la sommatoria (2), vediamo un esempio. Per n = 6, la sommatoria (1) diventa:
mentre la sommatoria (2) diventa:
Il passo successivo è considerare le doppie sommatorie, costituite da due sommatorie, una interna e una esterna, ognuna delle quali ha una variabile diversa che varia all’interno di un proprio insieme di valori. Esistono diversi tipi di doppie sommatorie, ma ci interessano maggiormente quelle dove la variabile della sommatoria più interna è limitata da quella della sommatoria più esterna, come nel caso seguente:
Calcolare questa sommatoria significa far variare i tra 1 ed n, per ciascun valore di i far variare j tra 1 ed i, calcolare il valore di f(i, j) per ogni coppia (i, j) così ottenuta, e alla fine sommare il tutto.
Considerando solamente i divisori di n, si ottiene la seguente sommatoria, analoga alla (1′):
Calcolare questa sommatoria significa far variare d nell’insieme dei divisori di n, per ciascun valore di d far variare d^{\prime} nell’insieme dei divisori di d, calcolare per ogni coppia (d, d^{\prime}) il valore di f(d, d^{\prime}), e alla fine sommare il tutto.
Per n = 6, la sommatoria (1′) diventa:
mentre la sommatoria (2′) diventa:
Ci sono poi delle doppie sommatorie che a prima vista possono sembrare sommatorie singole, perché il simbolo di sommatoria (\Sigma) compare solo una volta, ma è più corretto considerarle doppie, perché gli indici sono comunque due. Un esempio è il seguente:
Sommatorie estese a coppie di variabili aventi prodotto costante
Sia n un numero intero positivo. Si definisce il seguente simbolo:
La Figura 1 aiuta a capire cosa significa considerare tutte le coppie di indici a e b aventi prodotto costante (si è scelto n = 10).
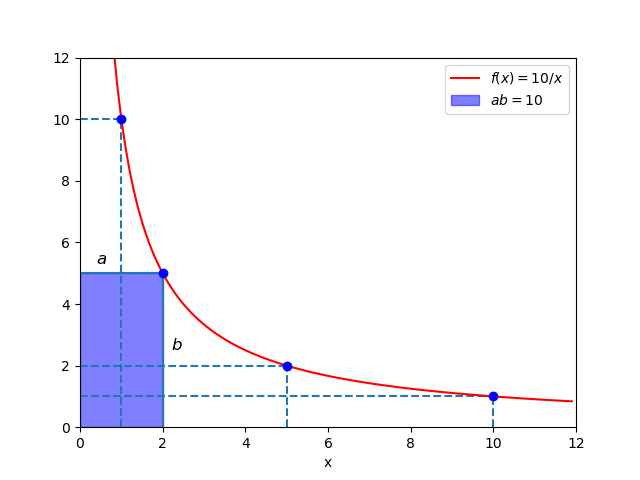
Se sostituiamo il simbolo di uguaglianza con il simbolo di divisibilità, otteniamo un altro tipo di sommatoria abbastanza ricorrente in teoria dei numeri:
Sommatorie estese a coppie di variabili il cui prodotto divide una costante
Sia n un numero intero positivo. Si definisce il seguente simbolo:
Questo tipo di sommatoria è un po’ più difficile da visualizzare, ma lo faremo a breve, dopo aver visto una proprietà che consente di scrivere la sommatoria in modo diverso.
Esiste infine una terza variante di questo tipo di sommatoria, col segno di \leq:
Sommatorie estese a coppie di variabili con prodotto minore o uguale a una costante
Sia n un numero intero positivo. Si definisce il seguente simbolo:
La Figura 2 aiuta a capire cosa significa considerare tutte le coppie di indici a e b aventi prodotto minore o uguale ad una costante (come per la Figura 1, si è scelto n = 10).
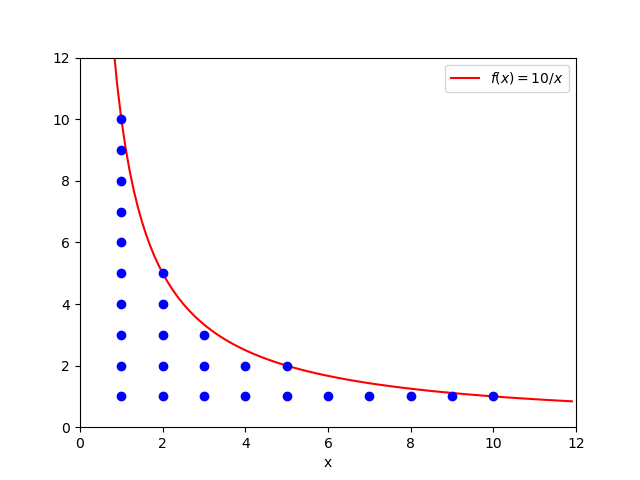
Le definizioni date finora possono essere estese al caso delle produttorie. Esse sono un modo compatto per denotare il prodotto di un certo numero di fattori, anziché la somma di un certo numero di addendi, e si indicano col simbolo di Pi greco maiuscolo (\Pi). Ad esempio, la (1) nel caso delle produttorie diventa:
che significa:
cioè il prodotto di tutti i fattori del tipo f(i), per i che varia tra 1 ed n.
Per estendere le nostre definizioni al caso delle produttorie, basta sostituire il simbolo di sommatoria (\Sigma) con quello di produttoria (\Pi) e l’operazione di somma con quella di prodotto. Ad esempio, riprendendo la Definizione N.20 si può definire:
Le nuove definizioni che si otterrebbero in questo modo non ci serviranno nel seguito, perciò le ometteremo in questo articolo, tuttavia per completezza abbiamo definito anche i simboli con le produttorie, assieme ai corrispondenti con le sommatorie, nella pagina Definizioni e simboli di teoria dei numeri.
Per chiudere questo elenco di simboli, introduciamo una convenzione che si usa molto in teoria dei numeri: quando l’indice di una sommatoria parte da 1, spesso si dà questo valore per sottinteso, evitando di scriverlo:
Sommatorie che partono da 1
Sia x un intero positivo. Si definisce il seguente simbolo:
Nei paragrafi successivi vedremo alcune proprietà di uso comune che riguardano i tipi di sommatorie che sono stati definiti in questo paragrafo.
Sommatorie dove il prodotto degli indici è uguale a una costante
Esiste un legame tra le sommatorie dove il prodotto degli indici è uguale a una costante e quelle estese ai divisori di un certo numero:
Forma equivalente per le sommatorie in cui compaiono d ed \frac{n}{d}
Sia n un numero intero positivo. Sia f una qualunque funzione definita su \mathbb{N}^{\star} \times \mathbb{N}^{\star} (non importa l’insieme di arrivo(*)). Allora:
(*) Per la precisione, è necessario che sull’insieme di arrivo siano definite l’operazione di somma e di prodotto, e che esse siano commutative. Tuttavia in questo contesto è inutile porsi il problema, perché ciò è vero per gli insiemi numerici che ci interessano (\mathbb{N}, \mathbb{Z} ed \mathbb{R}).
La tecnica dimostrativa che utilizzeremo per tutte le proprietà di questo articolo consiste nel far vedere che tutti i termini della sommatoria di destra compaiono anche nella sommatoria di sinistra, e viceversa.
Consideriamo un termine della sommatoria di destra, ossia f\left(d, \frac{n}{d}\right), per qualche d fissato, divisore di n. Ponendo a := d e b := \frac{n}{d}, si ha che a e b sono due interi positivi tali che ab = n, quindi la sommatoria di sinistra conterrà il termine f(a,b). Ma f(a, b) = f\left(d, \frac{n}{d}\right), cioè f(a,b) è proprio il termine che avevamo scelto sulla destra. Dato che questo ragionamento si può ripetere per ogni valore della variabile d della sommatoria di destra, abbiamo che tutti i termini della sommatoria di destra compaiono anche in quella di sinistra.
Consideriamo ora un termine della sommatoria di sinistra, ossia f(a, b), dove a e b sono due interi positivi tali che ab = n. Osserviamo che, per quest’ultima uguaglianza, a è un divisore di n e b = \frac{n}{a}. Allora, ponendo d := a, abbiamo che f(a, b) = f\left(a, \frac{n}{a}\right) = f\left(d, \frac{n}{d}\right), per cui il termine f(a, b) che avevamo scelto nella sommatoria di sinistra compare anche in quella di destra. Dato che questo ragionamento si può ripetere per ciascun termine della sommatoria di sinistra, abbiamo che tutti i termini della sommatoria di sinistra si trovano anche in quella di destra. Questo completa la dimostrazione.
Sommatorie dove il prodotto degli indici è minore o uguale a una costante
Le sommatorie dove il prodotto degli indici è minore o uguale a una costante possono essere ricondotte a quelle dove il prodotto degli indici è uguale a una costante:
Forma equivalente per le sommatorie dove il prodotto degli indici è minore o uguale di una costante
Sia n un numero intero positivo. Sia f una qualunque funzione definita su \mathbb{N}^{\star} \times \mathbb{N}^{\star} (non importa l’insieme di arrivo(*)). Allora:
(*) Valgono le stesse considerazioni fatte per la Proprietà N.14
La dimostrazione di questa Proprietà parte dall’osservazione che entrambe le sommatorie considerano i valori di f(a, b) per tutte le coppie di interi positivi a e b il cui prodotto è minore o uguale ad n, ma mentre la prima sommatoria non specifica l’ordine in cui sommare i termini, la seconda li ordina rispetto al prodotto ab, a cui si dà il nome k.
Infatti, consideriamo un termine f(a, b) della sommatoria di sinistra, quindi tale che ab \leq n. Ponendo k := ab, troveremo k nella sommatoria \sum_{k \leq n} e, essendo ab = k, troveremo il termine f(a, b) anche nella sommatoria di destra. Viceversa, considerando un termine f(a, b) della sommatoria di destra, abbiamo che ab = k e k \leq n, quindi ab \leq n, perciò il termine f(a, b) che avevamo scelto è presente anche nella sommatoria di sinistra. Quindi le due sommatorie hanno complessivamente gli stessi termini, e pertanto i loro valori coincidono.
Esiste anche un altro modo in cui le sommatorie di questo tipo possono essere riscritte:
Seconda forma equivalente per le sommatorie dove il prodotto degli indici è minore o uguale di una costante
Sia n un numero intero positivo. Sia f una qualunque funzione definita su \mathbb{N}^{\star} \times \mathbb{N}^{\star} (non importa l’insieme di arrivo(*)). Allora:
(*) Valgono le stesse considerazioni fatte per la Proprietà N.14.
Sia (a, b) una coppia di indici della doppia sommatoria di destra. Essendo \left\lfloor \frac{n}{a} \right\rfloor il quoziente della divisione di n per a, possiamo indicarlo con q e porre n := qa + r, dove r è il resto della stessa divisione. Allora b \leq \left\lfloor \frac{n}{a} \right\rfloor \Rightarrow b \leq q \Rightarrow ab \leq aq \leq n, quindi la coppia di indici (a, b) si troverà anche nella sommatoria di sinistra.
Viceversa, sia (a, b) una coppia di indici della sommatoria di sinistra, ossia tali che ab \leq n. Allora a \leq \frac{n}{b} \leq n; inoltre b \leq \frac{n}{a} ma, essendo un numero intero, deve essere b \leq \left \lfloor \frac{n}{a} \right \rfloor. Quindi la coppia di indici (a, b) compare anche nella sommatoria di destra.
In conclusione, le due sommatorie hanno esattamente gli stessi valori degli indici a e b e perciò, avendo anche lo stesso termine generale f(a, b), sono uguali.
Sommatorie dove il prodotto degli indici divide una costante
Le sommatorie dove il prodotto degli indici divide una costante possono essere ricondotte a quelle dove un singolo indice divide una variabile:
Prima forma equivalente per le sommatorie dove il prodotto degli indici divide una costante
Sia n un numero intero positivo. Sia f una qualunque funzione definita su \mathbb{N}^{\star} \times \mathbb{N}^{\star} (non importa l’insieme di arrivo(*)). Allora:
(*) Valgono le stesse considerazioni fatte per la Proprietà N.14
Sia (a, b) una coppia di indici della sommatoria \sum_{ab \mid n} f(a, b), quindi tali che ab \mid n. Affinché questi indici compaiano anche nella sommatoria di destra devono verificarsi, per qualche intero k, le seguenti condizioni:
- ak = n
- b \mid k
Certamente k non può che essere pari a \frac{n}{a}, per la prima equazione. Osserviamo che k := \frac{n}{a} è un numero intero, perché ab \mid n \Rightarrow a \mid n. Vediamo se questo valore di k soddisfa anche la seconda equazione. Partendo dall’ipotesi che ab \mid n, abbiamo che esiste un intero c tale che n = abc \Rightarrow \frac{n}{a} = bc \Rightarrow k = bc \Rightarrow b \mid k. Quindi è verificata anche la seconda equazione, perciò la coppia di indici (a, b) presi dalla sommatoria di sinistra compare anche nella sommatoria di destra. Si noti che, nella sommatoria di destra, il numero k non è un vero e proprio indice della sommatoria, perché non è utilizzato nel termine f(a, b), ma è solo di supporto per definire i valori di a e b.
Viceversa, sia (a, b) una coppia di indici della sommatoria \sum_{ak = n} \sum_{b \mid k} f(a, b). Quindi esiste un intero k tale che ak = n e b \mid k. Affinché gli indici a e b compaiano anche nella sommatoria di sinistra, si deve avere che ab \mid n. Considerando le ipotesi ak = n e b \mid k, si ha che k = bc per qualche intero c, e quindi n = ak = abc, da cui ab \mid n. Quindi la coppia di indici che abbiamo scelto compare anche nella sommatoria di sinistra.
In conclusione, le due sommatorie hanno esattamente gli stessi valori degli indici e perciò, avendo anche lo stesso termine generale f(a, b), sono uguali.
La Proprietà N.22 è visualizzata nella Figura 3.
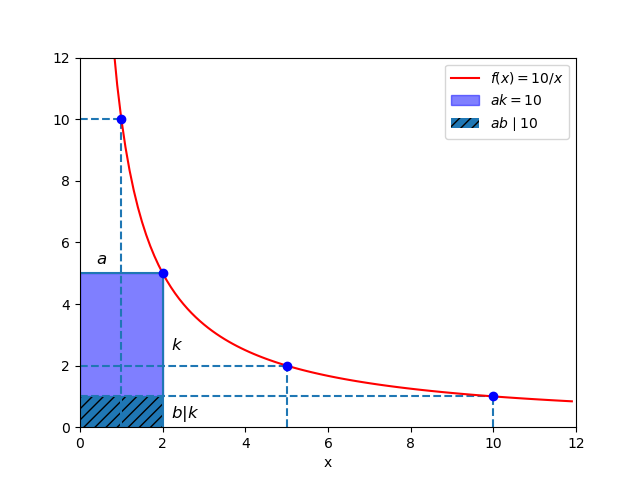
È possibile anche fare in modo di usare il simbolo di divisibilità per entrambi gli indici:
Seconda forma equivalente per le sommatorie dove il prodotto degli indici divide una costante
Sia n un numero intero positivo. Sia f una qualunque funzione definita su \mathbb{N}^{\star} \times \mathbb{N}^{\star} (non importa l’insieme di arrivo(*)). Allora:
(*) Valgono le stesse considerazioni fatte per la Proprietà N.14
La dimostrazione di questa Proprietà si ottiene da quella della Proprietà N.20, sostituendo il simbolo di divisibilità (\mid) al posto del simbolo di minore o uguale (\leq) e tenendo conto che, essendo b un divisore di n, \frac{n}{b} = \left\lfloor \frac{n}{b} \right\rfloor. In ogni caso, per maggiore chiarezza, riportiamo la dimostrazione valida per questa specifica Proprietà.
Sia (a, b) una coppia di indici della sommatoria \sum_{b \mid n} \sum_{a \mid \frac{n}{b}} f(a, b). Abbiamo che a \mid \frac{n}{b} \Rightarrow ab \mid n, quindi la coppia di indici (a, b) si troverà anche nella sommatoria \sum_{ab \mid n} f(a, b).
Viceversa, sia (a, b) una coppia di indici di quest’ultima sommatoria, ossia tali che ab \mid n. Allora anche b \mid n; inoltre ab \mid n \Rightarrow \exists c \text{ tale che } n = abc \Rightarrow \frac{n}{b} = \frac{abc}{b} = ac \Rightarrow a \mid \frac{n}{b}. Quindi la coppia di indici (a, b) compare anche nella sommatoria \sum_{b \mid n} \sum_{a \mid \frac{n}{b}} f(a, b).
In conclusione, le due sommatorie hanno esattamente gli stessi valori degli indici e perciò, avendo anche lo stesso termine generale f(a, b), sono uguali.
Valutiamo separatamente le sommatorie \sum_{ak = n} \sum_{b \mid k} f(a, b) e \sum_{b \mid n} \sum_{a \mid \frac{n}{b}} f(a, b) per n = 12:
Confrontando i risultati ottenuti, si può vedere che essi sono uguali a meno dell’ordine degli addendi, quindi la somma finale è la stessa. In particolare, sono presenti tutti e soli i termini del tipo f(a, b) tali che ab \mid 12, dunque entrambe le sommatorie coincidono con la sommatoria \sum_{ab \mid 12} f(a, b).
Esiste anche un terzo modo in cui possono essere riscritte le sommatorie di questo tipo:
Terza forma equivalente per le sommatorie dove il prodotto degli indici divide una costante
Sia n un numero intero positivo. Sia f una qualunque funzione definita su \mathbb{N}^{\star} \times \mathbb{N}^{\star} (non importa l’insieme di arrivo(*)). Allora:
(*) Valgono le stesse considerazioni fatte per la Proprietà N.14
Il principio che seguiremo è lo stesso di quello delle dimostrazioni delle Proprietà precedenti: per dimostrare che le due sommatorie sono uguali, dobbiamo verificare che ogni termine che compare a destra compare anche a sinistra, e viceversa.
Consideriamo un termine della sommatoria di sinistra. Esso è dato da f(a, b), dove a e b sono due interi positivi tali che ab \mid n. Vediamo se questo termine compare anche nella sommatoria di destra. Se così fosse, dovrebbero esistere due interi positivi d e d^{\prime} tali che:
- d \mid n
- d^{\prime} \mid d
- d^{\prime} = a
- \frac{d}{d^{\prime}} = b
Ma questi interi esistono, perché, come si può ricavare dalle ultime due equazioni, basta porre:
Questi valori di d e d^{\prime} soddisfano infatti anche le prime due equazioni, dato che per ipotesi ab \mid n. La corrispondenza (a) permette quindi di associare ad ogni possibile coppia di valori delle variabili (a, b) della sommatoria di sinistra, una coppia di valori per le variabili (d, d^{\prime}) che generano lo stesso termine nella sommatoria di destra.
Così abbiamo dimostrato che tutti i termini della sommatoria di sinistra compaiono in quella di destra; ora dobbiamo dimostrare il viceversa. Consideriamo quindi un termine della sommatoria di destra. Esso sarà del tipo f\left(d^{\prime}, \frac{d}{d^{\prime}}\right), dove d è un divisore di n e d^{\prime} è un divisore di d. Troveremo questo termine anche nella sommatoria di sinistra? Se così fosse, dovrebbero esistere due interi positivi a e b tali che:
- ab \mid n
- a = d^{\prime}
- b = \frac{d}{d^{\prime}}
I valori di a e b sono dati dalle ultime due equazioni:
Ma questi valori soddisfano anche la prima equazione, in quanto ab = d^{\prime} \frac{d}{d^{\prime}} = d \mid n.
Dunque, la corrispondenza (b) permette di associare ad ogni possibile coppia di valori delle variabili (d, d^{\prime}) della sommatoria di destra, una coppia di valori per le variabili (a, b) che generano lo stesso termine nella sommatoria di sinistra. Questo assicura che tutti i termini della sommatoria di sinistra compaiono in quella di destra, e completa la dimostrazione.
Vediamo un esempio con n = 12:
Alla fine abbiamo ottenuto la somma di tutti i possibili termini del tipo f(a, b), dove ab è un divisore di n, per cui la sommatoria iniziale si riduce alla forma seguente: