Prerequisiti:
- Il Teorema di Chebyshev (versione debole)
- Dai numeri interi ai numeri reali
- Dai numeri interi ai numeri reali – seconda parte
- Il fattoriale e la funzione \Lambda^{\star}
- Proprietà degli ordini asintotici
- Il teorema di Chebyshev (versione forte)
- Le funzioni W e V
- La media integrale e la funzione di errore assoluto R
- Alcune sommatorie importanti
- La funzione di Möbius e la sua connessione con la funzione \Lambda
- La formula di inversione di Möbius
- Due lemmi con la funzione di Möbius e il logaritmo
Dopo la digressione sulla funzione di Möbius degli ultimi tre articoli, torniamo alla dimostrazione del Teorema dei Numeri Primi. In questo articolo vedremo una delle parti più importanti della dimostrazione, che consiste nell’applicazione del Teorema di Selberg. Cercheremo di capire, tentando di ridurre al minimo i tecnicismi, perché questo Teorema riveste un ruolo così importante nella dimostrazione del Teorema dei Numeri Primi.
Nel Lemma N.7 abbiamo visto che una condizione sufficiente per dimostrare il Teorema dei Numeri Primi è: \limsup_{u \to +\infty} |V(u)| = 0. Nell’articolo La media integrale e la funzione di errore assoluto R, abbiamo chiamato \alpha questo limite superiore, e abbiamo iniziato a confrontarlo con il limite superiore della media integrale della stessa funzione, ossia con \beta := \limsup_{x \to +\infty} \frac{1}{\log x} \int_0^{\log x} |V(u)|\ du (v. Definizione N.14). Ci siamo chiesti quindi se, togliendo il limite superiore, per ogni intero x \gt 0 valga la relazione |V(\log x)| \leq \frac{1}{\log x} \int_0^{\log x} |V(u)|\ du, che per il Lemma N.8 è equivalente a:
Abbiamo visto che il Teorema di Selberg esprime una relazione asintotica in cui compaiono due termini simili ai due membri della (1):
In questo articolo vedremo come si arriva a questo Teorema e come esso viene utilizzato per dimostrare il Teorema dei Numeri Primi. Per rispondere a queste domande, utilizzeremo la conoscenza della funzione di Möbius.
Come si arriva al Teorema di Selberg?
Il Teorema di Selberg può essere considerato un risultato intermedio per arrivare alla formula (1), che, come abbiamo visto, è direttamente collegata al Teorema dei Numeri Primi.
Dalla formula (1) possiamo ottenere una formula simile, non equivalente ma più semplice da studiare, eliminando momentaneamente il valore assoluto e l’integrale. Quest’operazione è conveniente perché:
- Il valore assoluto verrà reintrodotto successivamente, nel Corollario 1 della Proposizione N.8;
- L’integrale può essere approssimato con una sommatoria, in questo caso del tipo \sum_{n \leq x} a_n R\left(\frac{x}{n}\right). È lo stesso principio che abbiamo applicato nell’articolo Dai numeri interi ai numeri reali – seconda parte, ma al contrario: in quel caso ci serviva introdurre gli integrali per applicare i teoremi di analisi matematica; qui invece ci serve eliminare gli integrali, per tentare di approssimare un’espressione più complessa con una più semplice. Una volta ottenuta una sommatoria che approssima l’integrale di partenza, nel prossimo articolo vedremo come stimare l’errore dovuto all’approssimazione.
Quindi per il momento accantoniamo la formula (1), in attesa di ritornarci nel prossimo articolo, e sostituiamola con la seguente:
Con queste semplificazioni, sviluppiamo separatamente i due termini della (1′). Per quanto riguarda il termine di sinistra, abbiamo che:
Utilizzando la definizione della funzione R e semplificando, abbiamo:
dove abbiamo utilizzato il fatto che, essendo x un numero intero, \overline{\psi}(x) = \psi(x).
Per la Proprietà N.6, \psi(x) = \sum_{n \leq x} \Lambda(n), quindi possiamo interpretare il termine \psi(x) \log x secondo il lemma dell’area dell’istogramma, ossia come la somma di tutte le basi dei rettangoli moltiplicata per l’altezza dell’ultimo rettangolo. Applicando questo Lemma con c_k := \Lambda(k), n := x e \widetilde{f}(t) := \log(t), si ottiene:
da cui:
Per il Teorema N.4, \psi(x) \asymp x, per cui anche \overline{\psi}(t) \asymp t. Allora, per la Definizione A.1, \overline{\psi}(t) = O(t) e quindi, per la Proprietà A.8A, \frac{\overline{\psi}(t)}{t} = O(1) (abbiamo visto anche il Teorema N.7, che dice di più sulla funzione \frac{\overline{\psi}(t)}{t}, ma qui ci basta sapere che è un O(1)). Sostituendo nella (b), abbiamo:
Nell’ultimo passaggio abbiamo applicato la Proprietà A.15, in quanto la funzione \frac{\overline{\psi}(t)}{t} è definita nell’intervallo [1, +\infty) ed è integrabile in ogni intervallo del tipo [1, b], con b \gt 1. L’integrabilità in [1, b], in particolare, si ha perché la funzione \frac{\overline{\psi}(t)}{t} può essere discontinua solo per i t dove la funzione \overline{\psi}(t) è discontinua, e questo può avvenire solo se t è un numero intero. Ma esiste un numero finito di interi in un intervallo limitato come [1, b], perciò la funzione può avere al massimo un numero finito di discontinuità in [1, b], dunque è ivi integrabile.
Infine, unendo le formule (a), (b) e (c) si ottiene la (3).
Per quanto riguarda il termine di destra della (1′), abbiamo detto che lo approssimeremo con una sommatoria del tipo \sum_{n \leq x} a_n R\left(\frac{x}{n}\right). Per capire quali coefficienti a_n conviene scegliere, svolgiamo alcuni passaggi:
A questo punto appare sensata la scelta a_n := \Lambda(n), in quanto:
- Per la Proprietà N.6, le funzioni \Lambda e \psi sono molto legate, e ciò può essere utile per semplificare la sommatoria \sum_{n \leq x} a_n \overline{\psi} \left( \frac{x}{n} \right) = \sum_{n \leq x} \Lambda(n) \overline{\psi} \left( \frac{x}{n} \right);
- La sommatoria \sum_{n \leq x} \frac{a_n}{n} = \sum_{n \leq x} \frac{\Lambda(n)}{n} è stimabile, mediante il Corollario della Proposizione N.7, come \log x + O(1).
Effettuando questa sostituzione nella (4), abbiamo:
dove negli ultimi due passaggi abbiamo applicato prima il Corollario 1 della Proprietà A.8 e poi la Proprietà N.20.
Osserviamo che in entrambe le formule (3) e (5) compare il termine x \log x, che quindi può essere eliminato sottraendo termine a termine (applicheremo anche le proprietà degli ordini asintotici Corollario 3 della Proprietà A.8 e Corollario della Proprietà A.9):
A questo punto entra in gioco la funzione di Möbius, che ci consente di esprimere queste sommatorie di \Lambda in modo più semplice:
Terzo lemma sulle sommatorie con la funzione di Möbius e il logaritmo
Sia x un numero intero positivo. Allora:
Partiamo dalla sommatoria più a sinistra. Per la Proprietà N.21, \sum_{nm \leq x} \Lambda(n) \Lambda(m) = \sum_{k \leq x} \sum_{nm = k} \Lambda(n) \Lambda(m). Scambiando i nomi delle variabili n e k, possiamo scrivere questa sommatoria come \sum_{n \leq x} \sum_{km = n} \Lambda(k) \Lambda(m). Dobbiamo quindi dimostrare che:
È evidente che la sommatoria \sum_{n \leq x} è ripetuta per ciascun termine. La strategia che seguiremo sarà perciò quella di dimostrare la (7′) senza questa sommatoria, ossia dimostrare che, per ogni n \gt 0:
Chiaramente, se questa uguaglianza è vera per ogni n, a maggior ragione è vera sommando ciascun membro per n = 1, \ldots, x, quindi è vera la (7′), che è equivalente alla (7).
Dimostriamo allora la (7”).
Partendo dal membro di sinistra, dato che come membro di destra vogliamo ottenere un’espressione che contiene solo la funzione di Möbius e il logaritmo, dobbiamo applicare le proprietà che ci consentono di esprimere la funzione \Lambda in termini delle altre due funzioni. Cominciamo ad applicare la Proprietà N.10 (forma logaritmica), per la quale:
Applicando le Proprietà N.22 e N.23, è possibile fare in modo che la sommatoria interna non abbia come indice d, ma k:
Abbiamo ottenuto così la sommatoria dei valori di \Lambda per tutti i divisori di \frac{n}{d}, che per la Proprietà N.17 è pari a \log \frac{n}{d}:
dove nell’ultimo passaggio abbiamo applicato nuovamente la Proprietà N.10 (forma logaritmica).
Unendo le formule (d), (e) ed (f) si ottiene:
che è equivalente alla (7”). Questo, come osservato inizialmente, conclude la dimostrazione.
La cosa interessante è che, come si può vedere in Figura 1, la funzione \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 d sembra essere molto simile alla funzione -x: se così fosse, dalla (6) si otterrebbe che \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) - R(x) \log x = \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 d + O(x) = O(x) + O(x) = O(x), dunque:
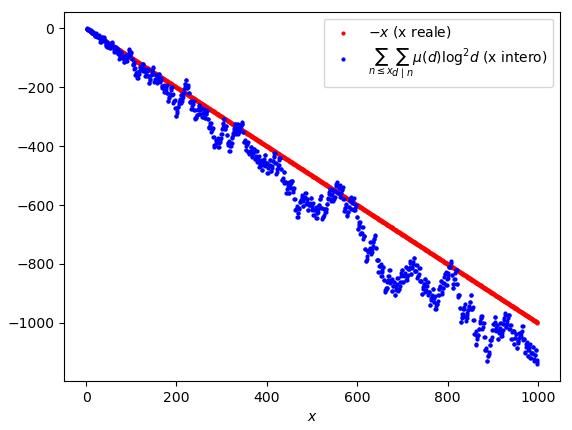
Questa relazione è identica al Teorema di Selberg, espresso dalla formula (2), a parte il segno del primo termine. Vedremo tra poco che non ci servirà dimostrare questa relazione, comunque riteniamo che si possa dimostrarla in modo simile ai Lemmi N.9 e N.10, ed invitiamo chi riesca a trovare la dimostrazione ad inviarcela.
Il motivo per cui abbiamo introdotto la formula (8), sebbene essa non sia effettivamente utilizzata nella dimostrazione del Teorema dei Numeri Primi, è che essa è utile per capire qual è l’idea di base. Infatti, riordinando i termini ed applicando la Proprietà A.6, la formula si può esprimere come segue:
da cui, introducendo il valore assoluto, si ottiene una relazione praticamente identica alla (1), salvo la sostituzione dell’integrale con una sommatoria:
Confrontando i valori dell’integrale (che per completezza rappresenteremo per valori reali di x) con quelli della sommatoria, si vede che l’approssimazione non è così male:
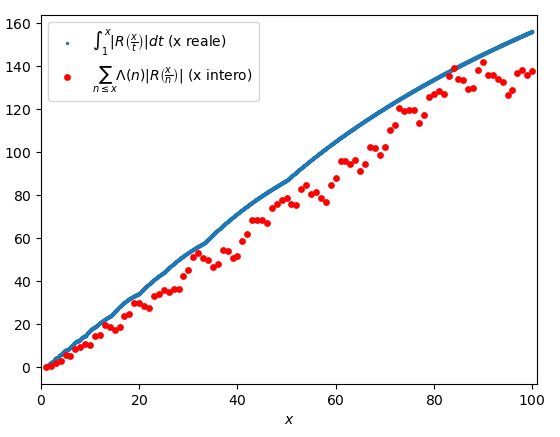
Sembrerebbe davvero un buon risultato, che ci potrebbe permettere di andare avanti con la dimostrazione del Teorema dei Numeri Primi; in realtà, però, le cose non stanno proprio così. I passaggi della dimostrazione sono molto simili a questi strutturalmente, ma sono un po’ più complessi. Ci sono, infatti, alcuni aspetti da considerare:
- Andando avanti con la dimostrazione, come vedremo nel prossimo articolo, ci si accorge che per proseguire serve moltiplicare ambo i membri della (9) per \log x.
- Questo passaggio di moltiplicazione per il logaritmo genera, nel membro di destra, dei nuovi coefficienti di R \left( \frac{x}{n} \right) la cui somma è proprio il membro di sinistra del Lemma N.11, che in valore assoluto è minore o uguale a \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n. Questo è il motivo per cui non ci serve conoscere l’ordine asintotico del membro di sinistra del Lemma N.11, ossia della differenza delle funzioni \sum_{nm \leq x} \Lambda(n) \Lambda(m) e \sum_{n \leq x} \Lambda(n) \log n, ma ci interessa quello della loro somma.
- Così come la differenza \sum_{nm \leq x} \Lambda(n) \Lambda(m) - \sum_{n \leq x} \Lambda(n) \log n presente nella (6) ha origine dalla differenza \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) - R(x) \log x, la somma \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n ha origine dalla somma \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) + R(x) \log x. Questo giustifica l’introduzione del Teorema di Selberg, che esprime l’ordine asintotico di quest’ultima somma, e quindi anche della somma \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n.
Dimostrazione e applicazione del Teorema di Selberg
Rimettendo tutto in ordine, quindi, i principali passaggi da effettuare per proseguire la dimostrazione del Teorema dei Numeri Primi sono i seguenti:
- Dimostrare il seguente Lemma:
Lemma alla base del Teorema di Selberg
Sia x un numero intero positivo. Allora:
\sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n = \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) \tag{10}Come abbiamo fatto per il Lemma N.11, dimostreremo la seguente uguaglianza ottenuta dalla (10) eliminando la sommatoria \sum_{n \leq x}:
\sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n = \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) \tag{10'}Per calcolare la somma di \sum_{km = n} \Lambda(k) \Lambda(m) e \Lambda(n) \log n, ci riconduciamo alla loro differenza, che per la formula (7”) della dimostrazione del Lemma N.11, è pari a \sum_{d \mid n} \mu(d) \log^2 d:
\begin{aligned} \sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n & = \\ \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n + 2 \Lambda(n) \log n & = \text{[per la (7'')]} \\ \sum_{d \mid n} \mu(d) \log^2 d + 2 \Lambda(n) \log n \end{aligned} \tag{g}Come abbiamo già fatto nella dimostrazione del Lemma N.11, applichiamo la Proprietà N.10 (forma logaritmica) per ottenere un’espressione contenente solo la funzione di Möbius e il logaritmo:
\begin{aligned} \sum_{d \mid n} \mu(d) \log^2 d + 2 \Lambda(n) \log n &= \\ \sum_{d \mid n} \mu(d) \log^2 d + 2 \left( - \sum_{d \mid n} \mu(d) \log d \right) \log n &= \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) \end{aligned} \tag{h}Osserviamo che \log^2 d - 2 \log d \log n sono due dei tre termini del quadrato di binomio (\log d - \log n)^2 = \log^2 d - 2 \log d \log n + \log^2 n. Il termine mancante, \log^2 n, non dipende da d, pertanto se ci fosse potrebbe essere portato fuori dalla sommatoria \sum_{d \mid n} \mu(d). Ma questa sommatoria, se n \gt 1, per la Proprietà N.11, è pari a zero! Questa osservazione ci consente di completare il quadrato di binomio, come segue:
\begin{aligned} \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) &= \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) + \log^2 n \cdot 0 &= \text{[$n \gt 1$]} \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) + \log^2 n \cdot \left( \sum_{d \mid n} \mu(d) \right) &= \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) + \sum_{d \mid n} \mu(d) \log^2 n &= \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n - \log^2 n) &= \\ \sum_{d \mid n} \mu(d) (\log d - \log n)^2 &= \\ \sum_{d \mid n} \mu(d) (\log n - \log d)^2 &= \\ \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) \end{aligned} \tag{i}I passaggi precedenti dimostrano che \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) = \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) per n \gt 1. Per completezza, bisogna dimostrare la stessa cosa per n = 1, osservando che in questo caso l’unico divisore d è 1 stesso:
\begin{aligned} n = 1 & \Rightarrow \\ \sum_{d \mid n} \mu(d) (\log^2 d - 2 \log d \log n) &= \\ \mu(1) (\log^2 1 - 2 \log 1 \log 1) &= \\ \mu(1) \cdot 0 &= \\ \mu(1) \log^2 \left( \frac{1}{1} \right) &= \\ \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) \end{aligned} \tag{i'}Unendo le formule precedenti si ottiene la (10′) e, analogamente alla dimostrazione del Lemma N.11, reintroducendo la sommatoria \sum_{n \leq x} si ottiene la (10).
-
Sulla base del Lemma N.12, applicando il Lemma N.10 si ottiene una stima asintotica della somma \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n:
Lemma alla base del Teorema di Selberg: stima asintotica
Sia x un numero intero positivo. Allora:
\sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n = 2x \log x + O(x)La dimostrazione si basa sul fatto che la sommatoria \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{n}{d} \right) che compare nell’enunciato del Lemma N.12 è molto simile alla sommatoria \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right) che conosciamo già: infatti, per il Lemma N.10, quest’ultima è pari a 2x \log x + O(x).
Partendo dalle formule (i) e (i’) della dimostrazione del Lemma N.12, modificando l’ultima formula in \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right) (quindi con x al posto di n nell’argomento del logaritmo) e sostituendo a ritroso \log x al posto di \log n in tutta la dimostrazione, si ottiene la seguente versione alternativa del Lemma N.12:
\sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log x = \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right) \tag{l}Per completare la dimostrazione del presente Lemma, quindi, non dobbiamo far altro che ricondurre la sommatoria \sum_{n \leq x} \Lambda(n) \log x alla sommatoria \sum_{n \leq x} \Lambda(n) \log n. Per fare ciò, riprendiamo le formule (b) e (c) presenti nel dettaglio sotto la formula (3), unendo le quali si ottiene:
\psi(x) \log x = \sum_{n \leq x} \Lambda(n) \log n + O(x)Ma, per la Proprietà N.6, \psi(x) = \sum_{n \leq x} \Lambda(n), per cui:
\sum_{n \leq x} \Lambda(n) \log x = \sum_{n \leq x} \Lambda(n) \log n + O(x)Ecco quindi il legame tra le sommatorie \sum_{n \leq x} \Lambda(n) \log n e \sum_{n \leq x} \Lambda(n) \log x.
Sostituendo all’interno della formula (l), otteniamo:\sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n + O(x) = \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right)Infine, applicando il Corollario 3 della Proprietà A.8 e il Lemma N.10, possiamo concludere la dimostrazione:
\begin{aligned} \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n & = \\ \sum_{n \leq x} \sum_{d \mid n} \mu(d) \log^2 \left( \frac{x}{d} \right) + O(x) & = \\ 2x \log x + O(x) \end{aligned} - Sulla base del Lemma N.13 si dimostra il Teorema di Selberg, di cui per comodità riproponiamo l’enunciato:
Teorema di Selberg
R(x) \log x + \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) = O(x)Sommando membro a membro le formule (3) e (5) ed applicando il Corollario della Proprietà A.9, abbiamo:
\begin{aligned} R(x) \log x + \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) &= \\ \sum_{n \leq x} \Lambda(n) \log n - x \log x + O(x) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) - x \log x + O(x) &= \\ \sum_{n \leq x} \Lambda(n) \log n + \sum_{nm \leq x} \Lambda(n) \Lambda(m) - 2x \log x + O(x) \end{aligned}Applicando il Lemma N.13 e nuovamente il Corollario della Proprietà A.9, abbiamo:
\begin{aligned} \sum_{n \leq x} \Lambda(n) \log n + \sum_{nm \leq x} \Lambda(n) \Lambda(m) - 2x \log x + O(x) &= \\ 2x \log x + O(x) - 2x \log x + O(x) &= \\ O(x) \end{aligned}Unendo le due formule precedenti si ottiene la tesi.
- Sulla base del Teorema di Selberg, si dimostra la seguente Proposizione:
Conseguenza del Teorema di Selberg
R(x) \log^2 x = O(x \log x) + \sum_{n \leq x} \left( \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n \right) R\left(\frac{x}{n} \right) \tag{11}La dimostrazione si basa su un gioco di somme e sottrazioni che, partendo da R(x) \log^2 x, consente di applicare ripetutamente il Teorema di Selberg, costruendo di volta in volta il termine mancante:
\begin{aligned} R(x) \log^2 x &= \\ \log x (R(x) \log x) &= \\ \log x \left( R(x) \log x + \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \right) - \log x \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) &= \text{[Teorema di Selberg]} \\ \log x \cdot O(x) - \log x \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) &= \\ \log x \cdot O(x) - \sum_{n \leq x} \left( \Lambda(n) R\left(\frac{x}{n}\right) \log x \right) &= \\ \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) (\log x - \log n + \log n) &= \\ \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n \tag{m} \end{aligned}Soffermiamoci ora sull’espressione R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) che compare nella sommatoria centrale. Potremmo porre y := \frac{x}{n} ottenendo R(y) \log y, espressione che potrebbe essere estesa come nella seconda uguaglianza sopra, ottenendo R(y) \log y + \sum_{n \leq y} \Lambda(n) R\left(\frac{y}{n}\right), consentendoci di applicare nuovamente il Teorema di Selberg. L’unico problema è che la sommatoria \sum_{n \leq y} è definita quando y è un numero intero, ma non è detto che y = \frac{x}{n} lo sia. Quindi potremmo porre y := \left \lfloor \frac{x}{n} \right \rfloor, commettendo un errore di:
R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) - R \left( \left \lfloor \frac{x}{n} \right \rfloor \right) \log \left \lfloor \frac{x}{n} \right \rfloorQui abbiamo un problema, perché stimare questo errore non è semplice. Questo problema però è facilmente aggirabile. Dai primi articoli fino ad ora, abbiamo supposto sempre che x sia un numero intero, pertanto abbiamo lavorato sempre con gli interi fin dove possibile, giustificando i motivi per cui a volte conviene passare ai numeri reali. Questo è un altro esempio di quando è richiesto questo passaggio: se per qualche ragione il numero x si trova ad essere diviso per un altro intero n che non è un suo divisore, il risultato non è un intero, per cui le formule che abbiamo ottenuto finora potrebbero non valere più, essendo state dimostrate partendo dall’assunzione che x sia intero. In realtà, fortunatamente, le nostre formule valgono lo stesso anche quando x non è intero, a patto di interpretare le sommatorie del tipo
\sum_{n \leq x}come
\sum_{n \leq \left \lfloor x \right \rfloor}con l’assunzione che x \geq 1.
Per essere sicuri che possiamo interpretare le sommatorie in questo modo, dovremmo in linea di principio ricontrollare tutte le dimostrazioni, ma ci limiteremo a un singolo esempio per capire il concetto. La dimostrazione della formula (3) inizia con questi passaggi:
\begin{aligned} R(x) \log x & = \\ (\overline{\psi}(x) - x) \log x & = \\ \overline{\psi}(x) \log x - x \log x \end{aligned}Se x non è intero, l’ultima espressione non è più uguale a \psi(x) \log x - x \log x, come abbiamo visto prima, ma è uguale a \psi(\left \lfloor x \right \rfloor) \log x - x \log x. Propagando questa modifica nella dimostrazione della formula (3), abbiamo che la parte intera di x va a finire proprio nella sommatoria \sum_{n \leq x} \Lambda(n) \log n, facendola diventare \sum_{n \leq \left \lfloor x \right \rfloor} \Lambda(n) \log n. Lo stesso discorso vale per tutti gli enunciati successivi, compreso il Teorema di Selberg, che per un numero reale t \geq 1 (dove t è l’argomento della funzione R, definita in [1, +\infty)) diventa:
R(t) \log t + \sum_{n \leq \left \lfloor t \right \rfloor} \Lambda(n) R\left(\frac{t}{n}\right) = O(t) \tag{n}Applicando questa versione “potenziata” del Teorema di Selberg all’espressione R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right), ponendo t := \frac{x}{n}, abbiamo che:
\begin{aligned} R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) &= \\ R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) + \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(m) R\left(\frac{x}{n} / m \right) - \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(m) R\left(\frac{x}{n} / m \right) &= \text{[per la (n)]}\\ O\left( \frac{x}{n} \right) - \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(m) R\left(\frac{x}{nm} \right) \end{aligned}Sostituendo nella (m), si ottiene:
\begin{aligned} \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log \left( \frac{x}{n} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) \left( O\left( \frac{x}{n} \right) - \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(m) R\left(\frac{x}{nm} \right) \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ \log x \cdot O(x) - \sum_{n \leq x} \Lambda(n) O\left( \frac{x}{n} \right) + \sum_{n \leq x} \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \end{aligned} \tag{o}Per la Proprietà N.20, \sum_{n \leq x} \sum_{m \leq \left \lfloor \frac{x}{n} \right \rfloor} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) = \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right). Inoltre, per le proprietà degli ordini asintotici Proprietà A.8A, Corollario 1 della Proprietà A.8 e Corollario della Proprietà A.9, \sum_{n \leq x} \Lambda(n) O\left( \frac{x}{n} \right) = x \cdot \sum_{n \leq x} \Lambda(n) O\left( \frac{1}{n} \right) = x \cdot \sum_{n \leq x} O\left( \frac{\Lambda(n)}{n} \right) = x \cdot O\left( \sum_{n \leq x} \frac{\Lambda(n)}{n} \right) . Quindi, il passaggio successivo è:
\log x \cdot O(x) - x \cdot O\left( \sum_{n \leq x} \frac{\Lambda(n)}{n} \right) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n =Ma, per il Corollario della Proposizione N.7, \sum_{n \leq x} \frac{\Lambda(n)}{n} = \log x + O(1), per cui O\left( \sum_{n \leq x} \frac{\Lambda(n)}{n} \right) = O\left( \log x + O(1) \right). Applicando in successione le proprietà degli ordini asintotici A.5, A.10, Corollario della Proprietà A.9 e Proprietà A.11, quest’ordine asintotico è pari a O(O(\log x) + O(1)) = O(O(\log x) + o(\log x)) = O(O(\log x) + O(\log x)) = O(O(\log x)) = O(\log x), per cui si ottiene:
\begin{aligned} \log x \cdot O(x) - x \cdot O(\log x) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ O(x \log x) - O(x \log x) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ O(x \log x) + \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n \end{aligned}Dove abbiamo semplificato gli ordini asintotici per mezzo delle proprietà Corollario 1 della Proprietà A.8, Corollario 3 della Proprietà A.8 e Corollario della Proprietà A.9.
Per la Proprietà N.21, \sum_{nm \leq x} \Lambda(n) \Lambda(m) R\left(\frac{x}{nm} \right) (che, rinominando n in k, è uguale a \sum_{km \leq x} \Lambda(k) \Lambda(m) R\left(\frac{x}{km} \right)), si può riscrivere come \sum_{n \leq x} \sum_{km = n} \Lambda(k) \Lambda(m) R\left(\frac{x}{n} \right), per cui abbiamo infine:\begin{aligned} O(x \log x) + \sum_{n \leq x} \sum_{km = n} \Lambda(k) \Lambda(m) R\left(\frac{x}{n} \right) - \sum_{n \leq x} \Lambda(n) R\left(\frac{x}{n}\right) \log n &= \\ O(x \log x) + \sum_{n \leq x} \left( \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n \right) R\left(\frac{x}{n}\right) \end{aligned}Ora, unendo la formula (m) con la formula (o) e quelle seguenti, si ottiene la tesi.
- Applicando il valore assoluto ad ambo i membri della (11), si ottiene il seguente Corollario:
Conseguenza del Teorema di Selberg
|R(x)| \log^2 x \leq \sum_{n \leq x} \left(\sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n\right) \left|R\left(\frac{x}{n}\right)\right| + O(x)Applicando il valore assoluto ad ambo i membri della (11), per la disuguaglianza triangolare si ha:
\begin{aligned} |R(x)| \log^2 x & \leq \\ |O(x \log x)| + \left| \sum_{n \leq x} \left( \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n \right) R\left(\frac{x}{n} \right) \right| & \leq \\ O(x \log x) + \sum_{n \leq x} \left| \sum_{km = n} \Lambda(k) \Lambda(m) - \Lambda(n) \log n \right| \left| R\left(\frac{x}{n}\right) \right| & \leq \\ O(x \log x) + \sum_{n \leq x} \left( \left| \sum_{km = n} \Lambda(k) \Lambda(m) \right| + \left| - \Lambda(n) \log n \right| \right) \left| R\left(\frac{x}{n} \right) \right| &= \\ O(x \log x) + \sum_{n \leq x} \left( \sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n \right) \left| R\left(\frac{x}{n} \right) \right| \end{aligned}Dove nella seconda uguaglianza abbiamo applicato la Proprietà A.6 e nell’ultimo passaggio abbiamo osservato che \Lambda è una funzione non negativa e anche il logaritmo assume valori non negativi, essendo n \geq 1. Concatenando le formule precedenti, si ottiene la tesi.
- Si può osservare che la somma dei coefficienti di \left|R\left(\frac{x}{n}\right)\right| nella Proposizione N.8, al variare di n, è proprio l’espressione che compare nel Lemma N.13, essendo \sum_{n \leq x} \left(\sum_{km = n} \Lambda(k) \Lambda(m) + \Lambda(n) \log n\right) = \sum_{nm \leq x} \Lambda(n) \Lambda(m) + \sum_{n \leq x} \Lambda(n) \log n, per la Proprietà N.21. Quindi, indicando l’n-esimo coefficiente con a_n, la Proposizione precedente può essere enunciata nella forma seguente:
Conseguenza del Teorema di Selberg, seconda forma
Per ogni intero positivo x, esistono dei numeri reali a_1, \ldots, a_x tali che \sum_{n \leq x} a_n = 2x \log x + O(x) e
|R(x)| \log^2 x \leq \sum_{n \leq x} a_n \left|R\left(\frac{x}{n}\right)\right| + O(x)
A questo punto, per concludere il nostro discorso sull’applicazione del Teorema di Selberg, dobbiamo ancora rispondere a due domande:
- Perché, nel passaggio dal Teorema di Selberg (Teorema N.10) alla Proposizione N.8, abbiamo moltiplicato per \log x?
- Se, come abbiamo visto in Figura 2, la sommatoria \sum_{n \leq x} \Lambda(n) \left|R\left(\frac{x}{n}\right)\right| approssima bene l’integrale \int_1^x \left| R\left(\frac{x}{t}\right) \right| dt, quale integrale è approssimato dalla sommatoria presente nei Corollari della Proposizione N.8?
Risponderemo a queste domande nel prossimo articolo.