Prerequisiti:
Il Teorema dei Numeri Primi è forse il più importante teorema che riguarda i numeri primi. È importante innanzitutto perché rappresenta il risultato di un’operazione tanto complessa quanto affascinante: far emergere l’ordine dal caos. È improprio parlare di caos in matematica, dove tutto si ottiene applicando regole ben precise, ma è anche vero che quando una successione numerica sfugge alla nostra immediata comprensione, molte volte essa ci sembra di natura caotica. Un esempio di tale successione è quella dei numeri primi. Infatti, esaminando una tavola dei numeri primi, è molto semplice notare come la loro distribuzione sembra sfuggire a qualsiasi regolarità; è più difficile invece osservare come dietro questa apparente irregolarità si celi un ordine ben preciso. Infatti, se è vero che le irregolarità sono evidenti quando si analizza la successione dei numeri primi nel dettaglio (ad esempio analizzando la differenza tra un numero primo ed il successivo), le cose cambiano quando la si osserva a livello più alto, nel suo complesso. Così facendo si può notare che l’andamento del numero di numeri primi minori o uguali ad un intero x, ossia il valore della funzione che abbiamo chiamato \pi(x), non è per nulla caotico, ma al crescere di x tende a conformarsi ad una funzione ben precisa e molto semplice: \frac{x}{\log x}. Il Teorema dei Numeri Primi dà a questo conformarsi un preciso significato matematico, quello di equivalenza asintotica:
Teorema dei Numeri Primi
Applicando la Definizione A.4 possiamo riscrivere l’enunciato del Teorema nella forma seguente:
Osservare che vale questo limite non è banale, ma richiede un certo sforzo di astrazione, anche perché ciò non è evidente empiricamente, nemmeno per numeri dell’ordine delle centinaia di milioni. Infatti, come abbiamo visto a proposito della versione forte del Teorema di Chebyshev, il rapporto \pi(x) / \frac{x}{\log x}, per x = 100.000.000 resta ancora al di sopra di 1,06:
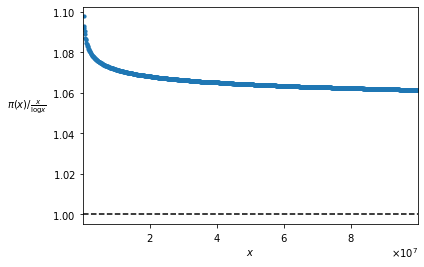
La formula (1) rende evidente la differenza tra il Teorema dei Numeri Primi e la versione forte del Teorema di Chebyshev. Infatti, l’unica differenza tra i due teoremi è che quello di Chebyshev non stabilisce l’esistenza del limite, ma si limita a dire che se il limite esiste, esso deve essere 1. Invece il Teorema dei Numeri Primi aggiunge il fatto che la funzione \pi(x) / \frac{x}{\log x} tende ad un limite, affermandone quindi l’esistenza.
Storia e aneddoti

Se già non è semplice verificare empiricamente il Teorema dei Numeri Primi, dimostrarlo è anche più difficile, anzi molto più difficile. La dimostrazione di questo teorema infatti è interessante di per sé, anche dal punto di vista storico, a cominciare dalle prime ricerche di Gauss sul finire del Settecento, passando per Jacques Hadamard e Charles de la Vallée Poussin, che trovarono una prima dimostrazione un secolo dopo, per finire con la cosiddetta dimostrazione “elementare”, che fu trovata da Paul Erdős e Atle Selberg nel 1949. Per descrivere questo excursus storico, utilizziamo le parole di Paul Hoffman, che ne L’uomo che amava solo i numeri lo racconta con diversi aneddoti, chiarendo nel contempo il significato del termine “elementare”:
La più grande vittoria sui numeri primi Erdős la ottenne nel 1949, anche se non amava parlarne, perché anch’essa fu una vittoria inquinata da polemiche. Se i matematici non dispongono di alcun metodo efficace per dire esattamente dove i primi si trovino, conoscono tuttavia fin dal tardo XVIII secolo una formula che ne descrive la distribuzione statistica, mostrando come in media si diradino con l’avanzare lungo i numeri. Alla ricerca di una formula del genere, Carl Friedrich Gauss, probabilmente il più grande matematico di tutti i tempi, iniziò a studiare le tavole dei numeri primi nel 1792, a quindici anni. […] La durezza del lavoro spinse Gauss a proporre la prima formula che predicesse la distribuzione dei primi, ma, benché essa trovasse convalida nel lungo elenco di primi conosciuti, il matematico non dimostrò mai che il suo Teorema dei Numeri Primi fosse vero universalmente. Passò un secolo prima che una sua dimostrazione venisse prodotta da Jacques Hadamard e Charles de la Vallée Poussin. […] Avanzata nel 1896, si affidava a un pesante armamentario, e le migliori menti matematiche erano convinte che non si sarebbe potuto giungervi con niente di meno. Erdős e Selberg, un suo collega non ancora pervenuto alla notorietà, sbalordirono il mondo della matematica con una dimostrazione “elementare”.
Tecniche elementari non significano necessariamente più semplici. In questo contesto “elementare” vuol dire che la dimostrazione della formula si basa su un ristretto insieme di numeri, i cosiddetti numeri reali, costituiti da numeri interi, numeri razionali e numeri irrazionali. […] Non sono ammessi i cosiddetti numeri immaginari come \sqrt{-1}, noto anche come i.[…] Erdős non aveva obiezioni filosofiche ai numeri immaginari; semplicemente, preferiva limitare il suo strumentario ai più familiari interi, ai razionali e agli irrazionali. Era il maestro dei metodi elementari. Quando, nel 1934, fece visita ad Hardy, quest’ultimo credeva che il Teorema dei Numeri Primi non si sarebbe mai arreso a metodi elementari e, se vi si fosse arreso, che si sarebbero dovuti buttar via e riscrivere da capo tutti i testi di teoria dei numeri. Hardy morì nel 1949, pochi mesi prima che Erdős e Selberg utilizzassero metodi elementari per far fuori il Teorema dei Numeri Primi.
Secondo gli amici di Erdős, i due concordarono di pubblicare i loro saggi fianco a fianco su una rivista di primo piano delineando i rispettivi contributi alla dimostrazione. A quel punto Erdős iniziò a spedire cartoline ai matematici informandoli che lui e Selberg avevano conquistato il Teorema dei Numeri Primi. Ma Selberg, a quanto pare, s’imbatté in un matematico che non conosceva e che aveva ricevuto la cartolina, e si sentì dire “Ha saputo? Erdős e Come-si-chiama hanno una dimostrazione elementare del Teorema dei Numeri Primi”. Ne rimase talmente offeso, si racconta, che si mosse subito da solo e pubblicò il suo saggio senza Erdős, accaparrandosi così la maggior parte del merito della dimostrazione. A lui solo fu assegnata nel 1950 la Fields Medal, l’equivalente del premio Nobel per la matematica, e in larga misura per il suo lavoro sul Teorema dei Numeri Primi.
Alla fine i testi di teoria dei numeri non sono stati riscritti tutti daccapo, come pensava Hardy, forse perché la dimostrazione di Erdős e Selberg è sì elementare dal punto di vista delle tecniche impiegate, ma molto complessa nella struttura. Forse Hardy, quando fece quell’affermazione, immaginava una dimostrazione allo stesso tempo elementare nelle tecniche e anche abbastanza semplice nella struttura, e si sarebbe in parte ricreduto se avesse visto quella di Erdős e Selberg. Nonostante ciò, questa dimostrazione suscitò grande scalpore quando fu pubblicata e resta ancora oggi di grande interesse per le tecniche impiegate. Tentando di cogliere lo spirito di Hardy, nei seguenti articoli tenteremo di riscriverla, in modo che appaia chiaro quali sono i passaggi principali e perché in certi punti risulti necessario utilizzare tecniche particolari. Così forse Erdős, il “maestro dei metodi elementari”, potrà insegnarci qualcosa sui metodi elementari che normalmente non rientra nei programmi dei corsi universitari. Abbiamo voluto dedicare a lui l’immagine principale di questo articolo, per contribuire a riscattarlo dalla presa di posizione di Selberg, il quale, come abbiamo visto, decise di pubblicare la dimostrazione senza il suo collega.
Per chi volesse approfondire il punto di vista storico sul Teorema dei Numeri Primi, segnaliamo questo interessante articolo di D. Goldfeld: The elementary proof of the prime number Theorem: an historical perspective.
Versione forte
Come per il Teorema di Chebyshev, anche per il Teorema dei Numeri Primi esiste una forma più forte, dove la funzione che approssima \pi(x) si chiama \mathrm{Li}(x):
Teorema dei Numeri Primi, versione forte
Dove Li sta per Logarithmic integral e la funzione \mathrm{Li} è definita come segue:
Funzione \mathrm{Li}: integrale logaritmico
Si definisce la funzione \mathrm{Li}: \mathbb{N}^{\star} \rightarrow \mathbb{R}, detta integrale logaritmico, tale che per ogni x \in \mathbb{N}^{\star}:
Il Teorema N.9 è una versione più forte del Teorema N.8 per due ragioni:
- Come sempre, la versione forte implica quella debole: se si dimostra la prima, automaticamente risulta dimostrata anche la seconda. In questo caso si può dimostrare che \mathrm{Li}(x) \sim \frac{x}{\log x}, quindi se vale la versione forte del Teorema dei Numeri Primi, ossia se \pi(x) \sim \mathrm{Li}(x), allora per transitività \pi(x) \sim \frac{x}{\log x}, cioè vale la versione debole.
Per capire perché \mathrm{Li}(x) \sim \frac{x}{\log x}, bisogna partire dalla seguente espressione asintotica di \mathrm{Li}(x):\mathrm{Li}(x) \sim \frac{x}{\log x} \sum_{k=0}^{\infty} \frac{k!}{(\log x)^k} = \frac{x}{\log x} + \frac{x}{(\log x)^2} + \frac{2x}{(\log x)^3} + \frac{6x}{(\log x)^4} + \ldots \tag{2}La dimostrazione di questa formula richiede parecchia teoria, che per ora lasciamo da parte. Dando per buona la (2), per la Definizione A.4 abbiamo che:
\lim_{x \to \infty} \left( \frac{x}{\log x} + \frac{x}{(\log x)^2} + \frac{2x}{(\log x)^3} + \frac{6x}{(\log x)^4} + \ldots \right) / \mathrm{Li}(x) = 1 \tag{3}Per dimostrare che \mathrm{Li}(x) \sim \frac{x}{\log x}, dobbiamo dimostrare che \lim_{x \to \infty} \frac{x}{\log x} / \mathrm{Li}(x) = 1. Questo deriva dal fatto che i termini dal secondo in poi che compaiono al numeratore della (3) hanno un ordine di grandezza inferiore rispetto al primo termine, pertanto sono ininfluenti ai fini del calcolo del limite.
Vediamo i passaggi nel dettaglio. Possiamo riscrivere la (3) come segue (per brevità scriveremo semplicemente \lim invece di \lim_{x \to \infty}):
\begin{aligned} \lim \left( \left( \frac{x}{\log x} + \frac{x}{(\log x)^2} + \frac{2x}{(\log x)^3} + \frac{6x}{(\log x)^4} + \ldots \right) / \frac{x}{\log x} \right) \cdot \left( \frac{x}{\log x} / \mathrm{Li}(x) \right) = 1 & \Leftrightarrow \\ \lim \left( \begin{gathered} \frac{x}{\log x} / \frac{x}{\log x} + \frac{x}{(\log x)^2} / \frac{x}{\log x} + \\ \frac{2x}{(\log x)^3} / \frac{x}{\log x} + \frac{6x}{(\log x)^4} / \frac{x}{\log x} + \\ \ldots \end{gathered} \right) \cdot \left( \frac{x}{\log x} / \mathrm{Li}(x) \right) = 1 & \Leftrightarrow \\ \lim \left( 1 + \frac{1}{\log x} + \frac{2}{(\log x)^2} + \frac{6}{(\log x)^3} + \ldots \right) \cdot \left( \frac{x}{\log x} / \mathrm{Li}(x) \right) = 1 \end{aligned} \tag{4}I limiti dei termini \frac{1}{\log x}, \frac{2}{(\log x)^2}, \frac{6}{(\log x)^3}, … sono tutti nulli, per cui il limite di tutta la serie tra parentesi esiste ed è 1. Se chiamiamo questa serie S, per la (4) abbiamo che \lim S \cdot \frac{x}{\log x} / \mathrm{Li}(x) = 1. Ma noi sappiamo che \lim S = 1, per cui dal limite del prodotto S \cdot \frac{x}{\log x} / \mathrm{Li}(x) possiamo ricavare il limite dell’altro fattore:
\lim \frac{x}{\log x} / \mathrm{Li}(x) = \lim \frac{S \cdot \frac{x}{\log x} / \mathrm{Li}(x)}{S} = \frac{\lim S \cdot \frac{x}{\log x} / \mathrm{Li}(x)}{\lim S} = \frac{1}{1} = 1Quindi \lim \frac{x}{\log x} / \mathrm{Li}(x) = 1, ossia \mathrm{Li}(x) \sim \frac{x}{\log x}.
- Inoltre, la seconda ragione per cui il Teorema N.5 è una versione più forte del Teorema N.8 è che il rapporto tra \pi(x) e \mathrm{Li}(x) tende ad 1 molto più velocemente di quanto lo faccia il rapporto tra \pi(x) e \frac{x}{\log x} (su Wikipedia è presente una tabella di confronto).
In apparenza potrebbe sembrare strano che due funzioni diverse, \mathrm{Li}(x) e \frac{x}{\log x}, siano asintoticamente equivalenti alla stessa funzione \pi(x). Il caso dei polinomi può aiutarci a comprendere meglio questa situazione. Per la Definizione A.2, due polinomi sono asintoticamente equivalenti quando hanno lo stesso grado e lo stesso coefficiente direttore, cioè lo stesso termine di grado massimo. Ad esempio i polinomi 2x^3 e 2x^3 + x^2 - 3 sono asintoticamente equivalenti, pur essendo diversi. Possiamo dire che i termini di grado inferiore a quello massimo sono ininfluenti dal punto di vista dell’equivalenza asintotica. La stessa cosa accade per le funzioni \frac{x}{\log x} e \mathrm{Li}(x). Quest’ultima infatti, per la (1), è data dalla prima più una serie di termini di “grado” inferiore, ossia aventi un ordine di grandezza più basso. Perciò le due funzioni, come accade per i polinomi 2x^3 e 2x^3 + x^2 - 3, sono asintoticamente equivalenti tra loro; quindi, tornando al discorso di prima, se si dimostra che una delle due è asintoticamente equivalente a \pi(x), per transitività lo è anche l’altra.
Per alcuni autori il “Teorema dei Numeri Primi” è il Teorema N.9, ossia la forma forte. Questa è in realtà la prima forma del Teorema che è stata dimostrata, da parte di Hadamard e de la Vallée Poussin, come abbiamo visto nel paragrafo precedente. La versione dimostrata da Erdős e Selberg in modo “elementare” invece è quella debole, per cui nei prossimi articoli ci concentreremo su quest’ultima.