Prerequisiti:
- Il lemma dell’area dell’istogramma
- Integrali e loro proprietà
- Teorema fondamentale del calcolo integrale
- Funzioni continue
- Classe C di una funzione
Finora abbiamo definito e studiato solamente funzioni definite su numeri interi, a valori interi (come le funzioni \theta(x) e \psi(x)) o reali (come le funzioni \theta^{\star}(x) e \psi^{\star}(x)). Si potrebbe pensare che questa cosa sia ovvia, essendo il nostro scopo lo studio dei numeri interi, in particolare dei numeri primi. Tuttavia, come spesso accade in matematica, per poter studiare una determinata classe di oggetti è spesso utile rifarsi ad una classe più ampia, mediante un processo di astrazione. Così, per studiare i numeri interi, vedremo che è utile rifarsi ai numeri reali. Ciò significa, in pratica, estendere il dominio di una funzione dai numeri interi ai numeri reali: un salto non indifferente. Vediamo due modi per farlo.
Estensione semplice
Consideriamo una funzione f definita su un insieme I di numeri interi (supponiamo in generale I \subseteq \mathbb{Z}). A partire da f definiamo sui numeri reali una nuova funzione \overline{f}, tale che:
- Per ogni intero n \in I, \overline{f}(n) = f(n)
- Per i numeri reali maggiori di n, fino al successivo intero n + 1 non compreso, \overline{f} continua ad assumere il valore f(n)
Se confrontiamo i grafici delle due funzioni, possiamo vedere che la funzione f si presenta “puntiforme”, perché l’insieme di definizione è discreto, mentre la funzione \overline{f} si presenta “a gradini”. Ad esempio, per I = \{0, ..., 9\} ed f(n) = n abbiamo:
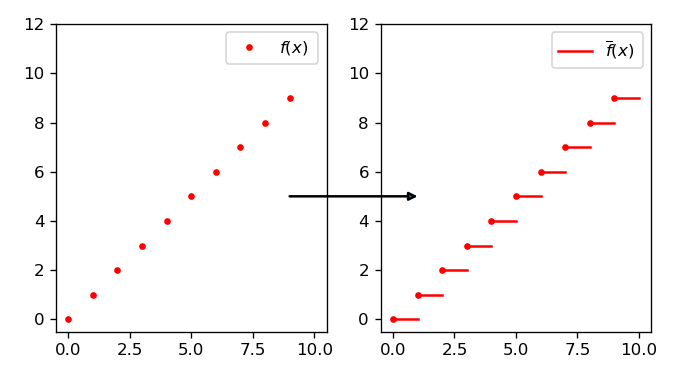
La funzione \overline{f} è definita su un insieme che possiamo chiamare \overline{I}, ottenuto da I aggiungendo ad esso, per ogni intero che vi appartiene, tutti i numeri reali fino al successivo intero escluso. Ad esempio:
| I | \overline{I} |
|---|---|
| \{0, 1, 2, 3\} | [0, 4) |
| \mathbb{N} | [0, +\infty) |
| \mathbb{N}^{\star} | [1, +\infty) |
| \mathbb{Z} | \mathbb{R} |
La definizione formale di estensione semplice è la seguente:
Estensione semplice di una funzione definita sui numeri interi, ai numeri reali
Sia f: I \rightarrow \mathbb{R} una funzione definita su un insieme I \subseteq \mathbb{Z}. Si definisce sull’insieme \overline{I} := \bigcup_{n \in I} [n, n+1) la funzione \overline{f}: \overline{I} \rightarrow \mathbb{R} tale che:
\forall n \in I\ \forall x \in [n, n+1): \overline{f}(x) := f(n) \tag{1}Chiameremo la funzione \overline{f} “estensione semplice di f ai numeri reali”, o semplicemente “estensione semplice di f“.
La formula (1) è la traduzione formale del fatto che \overline{f} assume lo stesso valore di f su qualsiasi intero n e sui numeri reali successivi, fino al successivo intero non compreso. La stessa cosa si può esprimere anche con la seguente definizione equivalente:
\overline{f}(x) := \begin{cases} f(x) & \text{se }x \in I \\ f(\left \lfloor x \right \rfloor) & \text{altrimenti }\end{cases} \tag{2}Questa formula dice sostanzialmente che:
- sugli interi, cioè sull’insieme I, f ed \overline{f} assumono lo stesso valore
- sugli altri numeri reali x, \overline{f} assume il valore assunto da f sull’intero immediatamente precedente ad x, ossia sulla parte intera di x
Ad esempio, \overline{f}(\frac{7}{2}) è il valore assunto da f sulla parte intera di \frac{7}{2}, ossia \left \lfloor \frac{7}{2} \right \rfloor = 3. La stessa cosa vale per tutti i reali nell’intervallo [3, 4), perché tutti hanno come parte intera 3: ripetendo questo ragionamento con un generico intero n al posto di 3, si può capire come la (2) sia equivalente alla (1).
Osserviamo che i valori assunti da \overline{f} sono, presi nel complesso, gli stessi assunti da f: infatti nella definizione (1) i valori di \overline{f} sono definiti mediante opportuni valori di f. In altri termini, le funzioni f ed \overline{f} hanno la stessa immagine: f(I) = \overline{f}(\overline{I}).
Abbiamo chiamato “semplice” l’estensione descritta nella Definizione N.8 non per indicare che sia “facile”, ma perché, se I è finito, l’estensione \overline{f} è una cosiddetta “funzione semplice”, ossia, semplificando, una funzione che assume un numero finito di valori. Le funzioni semplici si studiano in teoria della misura.
Estensioni generiche
La Definizione N.8 può sembrare artificiosa: si potrebbe pensare ottenere la funzione estesa definendola semplicemente allo stesso modo di f, ma sui numeri reali. Ad esempio si potrebbe estendere la funzione
f: \mathbb{N} \rightarrow \mathbb{R} \text{ t.c. } f(n) := nmediante la funzione
\widetilde{f}: \mathbb{R} \rightarrow \mathbb{R} \text{ t.c. } \widetilde{f}(x) := x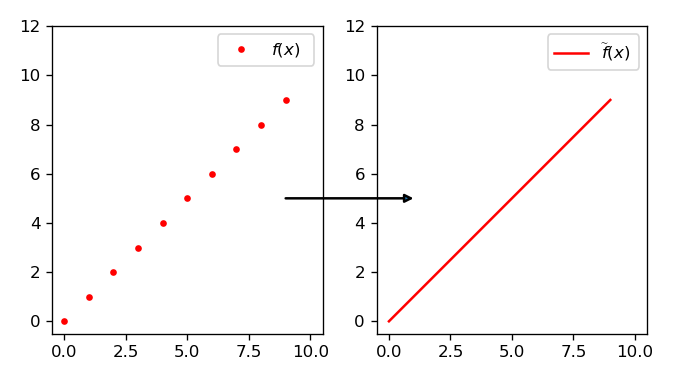
In pratica, la funzione originale e la funzione estesa condividono la stessa espressione formale (abbiamo solo messo x al posto di n, ma avremmo potuto usare anche lo stesso nome di variabile in entrambi i casi). Tuttavia non tutte le espressioni che hanno senso per i numeri interi, continuano ad averne quando si passa ai reali. Ad esempio, una definizione come:
g(x) := \text{numero di divisori di }xha perfettamente senso se x è un numero intero, ma non per un generico numero reale (quali sarebbero, ad esempio, i divisori di \sqrt{2}?). Per evitare problemi di questo tipo, non tenteremo di formalizzare l’idea di ottenere un’estensione mediante “un’espressione simile” a quella che definisce la funzione di partenza, sebbene questo sia ciò che accade in molti casi. Lasciamo invece volutamente generica la definizione di estensione, con l’unico vincolo che la funzione originale e quella estesa devono assumere, sugli interi, gli stessi valori:
Estensione di una funzione definita sui numeri interi, ai numeri reali
Sia f: I \rightarrow \mathbb{R} una funzione definita su un insieme I \subseteq \mathbb{Z}. Sia \overline{I} := \bigcup_{n \in I} [n, n+1) ed \widetilde{f}: \overline{I} \rightarrow \mathbb{R} una funzione tale che:
\widetilde{f}_{\mid I} = fDiremo che la funzione \widetilde{f} è una “estensione di f ai numeri reali”, o semplicemente una “estensione di f“.
Possiamo osservare che l’estensione semplice (Definizione N.8) è un caso particolare di estensione. Infatti per definizione \overline{f}(x) = f(n) per ogni n \in I e per ogni x \in [n, n+1); in particolare, per x := n si ha che \overline{f}(n) = f(n).
A livello grafico, abbiamo che il grafico di f è costituito da punti isolati (un punto per ogni n \in I), mentre il grafico di \widetilde{f} è una generica curva che passa per questi punti. Nel caso dell’estensione semplice (Figura 1), questa curva è data dall’unione di più segmenti staccati, segno che l’estensione non è continua, a differenza ad esempio dell’estensione della Figura 2.
Applicazione al lemma dell’area dell’istogramma
In teoria dei numeri si usano spesso le estensioni, perché consentono di applicare i teoremi dell’analisi reale a funzioni definite su numeri interi. In particolare, l’estensione semplice è utile quando una funzione definita sui numeri interi moltiplica un integrale, ed in tal caso permette di portare la funzione sotto il segno di integrale.
Un esempio di applicazione delle estensioni è il Lemma dell’area dell’istogramma:
A = \sum_{k = 1}^{n-1} C_k (f(k) - f(k + 1)) + C_n f(n) \tag{3}Infatti, nell’espressione a destra, la sommatoria può essere riscritta diversamente applicando il concetto di estensione.
Per prima cosa, estendendo la funzione f possiamo riscrivere il termine f(k) - f(k + 1) come \widetilde{f}(k) - \widetilde{f}(k + 1). A questo punto, ipotizzando che la funzione \widetilde{f} sia di classe C^1 in tutto \overline{I} (quindi in particolare nell’intervallo [k, k+1)), in modo che la sua derivata sia continua e quindi integrabile, possiamo applicare il Teorema fondamentale del calcolo integrale, ottenendo:
\widetilde{f}(k) - \widetilde{f}(k + 1) = - \int_k^{k+1} \widetilde{f}'(t) dt \tag{4}Ecco spiegato da dove nascono gli integrali nella teoria dei numeri: grazie al teorema fondamentale del calcolo integrale, una semplice differenza tra due numeri diventa un integrale. Questo passaggio può sembrare artificioso, ma vedremo che è essenziale per lo sviluppo della teoria.
Sostituendo la (4) nella formula (3) del Lemma, il termine generico della sommatoria diventa
- C_k \int_k^{k+1} \widetilde{f}'(t) dtLe costanti C_k, che rappresentano le somme delle basi dei primi k rettangoli dell’istogramma, essendo dipendenti da k, possono essere considerate complessivamente una funzione di k, ossia possiamo introdurre la funzione:
C: \{1, \ldots, n\} \rightarrow \mathbb{R} \text{ t.c. } C(k) := C_kQuesta funzione, che associa semplicemente a k la k-esima costante, ci permette di riscrivere il generico termine della sommatoria come
- C(k) \int_k^{k+1} \widetilde{f}'(t) dtOra possiamo effettuare una estensione semplice della funzione C, riscrivendo questo termine come
- \overline{C}(k) \int_k^{k+1} \widetilde{f}'(t) dt \tag{5}A questo punto abbiamo una funzione \overline{C} che per la (1) è costante sull’intervallo reale [k, k+1), che è proprio l’intervallo dei valori assunti dalla variabile di integrazione t. Questo ci permette di portarla sotto il segno di integrale sostituendo k con t, ottenendo:
- \int_k^{k+1} \overline{C}(t) \widetilde{f}'(t) dt \tag{6}Possiamo chiamare X il valore costante della funzione \overline{C} nell’intervallo [k, k+1) e, per le proprietà degli integrali, portarla sotto il segno di integrale:
- X \int_k^{k+1} \widetilde{f}'(t) dt = - \int_k^{k+1} X \widetilde{f}'(t) dtAbbiamo detto che la costante X rappresenta il valore assunto da \overline{C} in k, e perciò il membro di sinistra coincide con la (5), ma essa rappresenta anche il valore assunto dalla stessa funzione su tutti i punti dell’intervallo [k, k+1). Questi punti sono proprio i valori assunti dalla variabile di integrazione t, che varia tra k e k+1, con l’eccezione del singolo punto k + 1. Quindi l’integrale a destra si può riscrivere come:
- \int_{k}^{k+1} \left( \begin{cases} \overline{C}(t) & \text{se }t \in [k, k+1)\\ X & \text{se }t = k+1\end{cases} \right) \widetilde{f}'(t) dt \tag{5'}Ma all’interno di un integrale si può modificare la funzione integranda in un singolo punto senza che il risultato ne risenta, per cui al posto della funzione senza nome che compare nella (5′), quella tra parentesi, possiamo semplicemente utilizzare la funzione \overline{C}. Così facendo non cambia nulla nell’intervallo [k, k+1), mentre non importa se \overline{C}(k+1) sia uguale ad X o meno: in ogni caso il risultato finale dell’integrale non cambia. In questo modo si ottiene la (6).
Sostituendo la (6) al posto del generico termine della sommatoria nella (3), quest’ultima diventa:
A = C(n) f(n) - \sum_{k = 1}^{n-1} \int_k^{k+1} \overline{C}(t) \widetilde{f}'(t) dtEspandendo la sommatoria, questa formula si riscrive come:
A = C(n) f(n) - \left( \int_1^2 \overline{C}(t) \widetilde{f}'(t) dt + \int_2^3 \overline{C}(t) \widetilde{f}'(t) dt + \ldots + \int_{n-1}^n \overline{C}(t) \widetilde{f}'(t) dt \right)Poiché tutte le coppie di integrali consecutivi hanno un estremo in comune e la stessa funzione integranda, per le proprietà degli integrali essi possono essere riuniti in uno solo:
A = C(n) f(n) - \int_1^n \overline{C}(t) \widetilde{f}'(t) dt \tag{7}Abbiamo ottenuto così una nuova forma del Lemma dell’area dell’istogramma. Nel prossimo articolo vedremo il vantaggio di adottare di questa nuova forma rispetto alla precedente, giustificando così l’introduzione degli integrali.
Lemma dell’area dell’istogramma, seconda forma
Siano c_1, c_2, \dots, c_n dei numeri reali non negativi, con n > 0. Sia f: \{1, 2, ..., n\} \rightarrow \mathbb{R} una funzione, e sia \widetilde{f} una sua estensione di classe C^1. Allora l’area A dell’istogramma composto da n rettangoli, ciascuno avente base c_i ed altezza f(i), data da
A = c_1 f(1) + c_2 f(2) + \ldots + c_n f(n) = \sum_{i=1}^{n} c_i f(i)si può calcolare anche con la formula
C(n) f(n) - \int_1^n \overline{C}(t) \widetilde{f}'(t) dtdove C: \{1, 2, ..., n\} \rightarrow \mathbb{N} è la funzione definita da C(k) := c_1 + c_2 + \ldots + c_k = \sum_{i=1}^{k} c_i.
Nei testi di teoria dei numeri non troverete le nostre notazioni per le funzioni estese, come \overline{C} e \widetilde{f}: sono notazioni introdotte da noi, non universali. Normalmente non si usa nessuna notazione particolare per distinguere le funzioni estese dalle rispettive funzioni di provenienza, ad esempio la (7) sarebbe scritta come segue:
A = C(n) f(n) - \int_1^n C(t) f'(t) dtTuttavia riteniamo che sia bene distinguere, per maggiore chiarezza, tra funzioni che “nascono” definite solo su numeri interi, e le loro estensioni ai reali. Inoltre la notazione che abbiamo scelto per le estensioni semplici, come \overline{C}, grazie al segno di una linea orizzontale, aiuta a ricordare che si tratta di una funzione dal grafico “a gradini”, a differenza delle estensioni generiche, che normalmente sono funzioni continue.