Prerequisiti:
I coefficienti binomiali sono importanti per lo studio dei numeri primi, come vedremo nell’articolo Il prodotto dei primi numeri primi. Vediamo in dettaglio alcune loro proprietà, che serviranno per i nostri scopi. Si tratta di tre stime: una per eccesso e due per difetto. Il motivo della ricerca di una stima per i coefficienti binomiali è che la loro definizione si rivela particolarmente ostica da utilizzare sia nei calcoli che nei ragionamenti analitici: perciò molte volte è preferibile adoperare una stima, affetta da errore ma più facile da utilizzare, piuttosto che il valore esatto.
Le prime due si ottengono facilmente ricordando il nesso tra i coefficienti binomiali ed il cosiddetto triangolo di Tartaglia:
Questo triangolo ha molte proprietà interessanti, ben note nella matematica scolastica. Quelle che più ci interessano sono le seguenti:
- Numerando le righe a partire da 0, la somma dei numeri sulla riga n è 2^n
- Ogni riga è simmetrica: rimane identica se letta da destra verso sinistra o da sinistra verso destra
- Ogni numero diverso da 1 è la somma dei due numeri immediatamente sovrastanti
- Numerando anche i numeri sulle righe a partire da 0, da sinistra verso destra, il numero in posizione m sulla riga n, con n > 0, è il binomiale \binom{n}{m}
L’ultima proprietà, in particolare, indica il nesso tra il triangolo di Tartaglia ed i coefficienti binomiali. Infatti, per questa proprietà il triangolo può essere riscritto come segue:
Le proprietà del triangolo allora si riflettono immediatamente in altrettante proprietà dei coefficienti binomiali. Ad esempio, considerando la sesta riga, cioè la riga numero 5 partendo da 0, la prima proprietà dice che
ossia la somma dei numeri della riga è 2 elevato al numero della riga.
Questa proprietà, “tradotta” nei coefficienti binomiali, diventa
Ciò che però non è evidente in questa seconda formulazione, ma lo è nella (1), è che i binomiali che occupano posti simmetrici sono uguali (questo per la seconda proprietà): infatti, confrontando la (1) con la (2), abbiamo che:
Questa semplice osservazione è la base per la prima stima. Infatti, se ogni binomiale si ripete due volte su una riga, il suo doppio (cioè la somma delle due ripetizioni) è certamente minore o uguale alla somma della riga stessa, in questo caso 2^5. Ad esempio:
Dunque 2 \cdot \binom{5}{1} \leq 2^5, ossia \binom{5}{1} \leq 2^4, che è esattamente la prima proprietà (sebbene la dimostrazione sia da completare, perchè non sempre i numeri sono ripetuti due volte su una riga: nelle righe con un numero dispari di elementi vi è un numero centrale non ripetuto):
Maggiorazione dei binomiali
Per ogni n > 0 e per ogni m:
Non è necessario specificare che 0 \leq m \leq n, in quanto non potrebbe essere altrimenti, perché il binomiale \binom{n}{m} non è definito per altri valori di m.
Ripartiamo dalla (1), in cui abbiamo tre numeri distinti, 1, 5 e 10, ciascuno ripetuto due volte. La ripetizione è dovuta alla seconda proprietà, quella della simmetria: i numeri ripetuti si trovano infatti in posizioni opposte, rispetto ad un immaginario centro della riga. Raggruppando questi numeri ripetuti, dalla (1) possiamo ricavare una disuguaglianza per ciascuno di essi:
A questo punto saremmo tentati di dire che il doppio di un numero sulla riga n è minore o uguale della somma della riga, ossia di 2^n. Tuttavia non posiamo subito operare questa generalizzazione. Infatti nell’esempio di sopra ogni numero della riga è ripetuto due volte, ma, osservando il triangolo di Tartaglia, si vede che non tutti i numeri sono ripetuti, perciò restano da trattare questi casi. In particolare, le righe con un numero dispari di elementi, che sono le righe con n pari, hanno un elemento centrale che non è ripetuto. Un esempio è la riga 4:
In questo caso possiamo ripetere il ragionamento di prima per i numeri 1 e 4:
Dobbiamo capire però come dimostrare che 2 \cdot 6 \leq 2^4, in un modo che sia generalizzabile a tutti i numeri centrali delle righe con un numero dispari di elementi. Per farlo dobbiamo mettere in gioco la terza proprietà del triangolo di Tartaglia, una delle più note, secondo cui ogni numero diverso da 1 è la somma dei due numeri immediatamente sovrastanti. In questo caso 6 è la somma di 3 + 3, che sono i due numeri sovrastanti:
Ma 3 + 3 a sua volta è minore o uguale alla somma dei numeri della sua riga, per cui:
Moltiplicando per due, si ha che
che è esattamente la relazione che volevamo ottenere, corrispettiva della (4) e della (5). In questo caso n = 4 ma il ragionamento si può estendere al numero centrale della riga n per qualsiasi n pari maggiore di 0. Per la riga 0 il ragionamento non è applicabile perché non esiste una riga precedente a cui ricondursi, ed in effetti per questa riga la proprietà non vale (il numero centrale, 1, è anche l’unico numero della sua riga e quindi pari alla somma della riga; raddoppiandolo si ottiene un numero maggiore). Tuttavia non c’è da preoccuparsi di questo caso, perché la riga 0 non è importante per i nostri scopi, essendo i binomiali definiti per n > 0.
Ricapitolando, abbiamo dimostrato, sulla base delle prime tre proprietà, che il doppio di qualunque numero di una riga n del triangolo di Tartaglia, con n > 0, è minore o uguale a 2^n, che è la somma degli elementi della riga. Ma sappiamo, per l’ultima proprietà del triangolo di Tartaglia, che questi numeri sono i binomiali del tipo \binom{n}{m}, con m compreso tra 0 ed n. Allora abbiamo dimostrato che, per qualsiasi n > 0 e qualsiasi m,
da cui si ottiene Proprietà N.1.
Possiamo notare che, fissato n, la stima (3) è tanto più accurata quanto più \binom{n}{m} è grande, rispetto agli altri numeri della riga n (ricordiamo infatti che il membro di destra della (3) è la metà della somma dei numeri della riga n). Come si può vedere dal triangolo di Tartaglia, i numeri di una riga crescono andando verso il centro, quindi i binomiali \binom{n}{m} più grandi, fissato n, sono quelli dove m è più vicino ad \frac{n}{2}. In particolare, se n è pari, il binomiale più grande è \binom{n}{\frac{n}{2}}, come 6 = \binom{4}{2} nella riga 4; se n è dispari, i binomiali più grandi, uguali tra loro, sono \binom{n}{\left \lceil \frac{n}{2} \right \rceil} e \binom{n}{\left \lfloor \frac{n}{2} \right \rfloor}, come 10 = \binom{5}{2} = \binom{5}{3} nella riga 5. Quindi le stime più accurate sono:
per n pari, e
per n dispari. Saranno proprio queste ultime le stime che ci serviranno per lo studio dei numeri primi, nella pagina Il prodotto dei primi numeri primi.
Partendo dal fatto che i binomiali delle formule (6) e (7) siano i più grandi delle loro righe, con tecniche simili a quelle di prima si può ottenere una seconda stima, questa volta per difetto:
Minorazione dei binomiali centrali del triangolo di Tartaglia
Per ogni n \geq 2:
se n è pari, e
se n è dispari.
Cominciamo con un caso specifico. Considerando che il binomiale \binom{6}{3} è il più grande della settima riga, possiamo utilizzarlo per maggiorare ciascun elemento della riga, ottenendo:
Questi passaggi si generalizzano facilmente ad un generico n, ottenendo
per n pari, e
per n dispari.
Possiamo migliorare leggermente questa stima osservando che, dalla riga 2 del triangolo di Tartaglia in poi, il binomiale più grande della riga è maggiore o uguale a 2, e ciò ci permette di risparmiare una maggiorazione accorpando i due termini 1, ad esempio:
Generalizzando per un n generico, otteniamo la Proprietà N.2.
Notiamo che questa stima vale solo per i binomiali centrali delle righe del triangolo di Tartaglia, diversamente dalla proprietà precedente, che valeva per tutti i binomiali. La Proprietà N.2 sarà uno degli elementi necessari per la dimostrazione del Postulato di Bertrand.
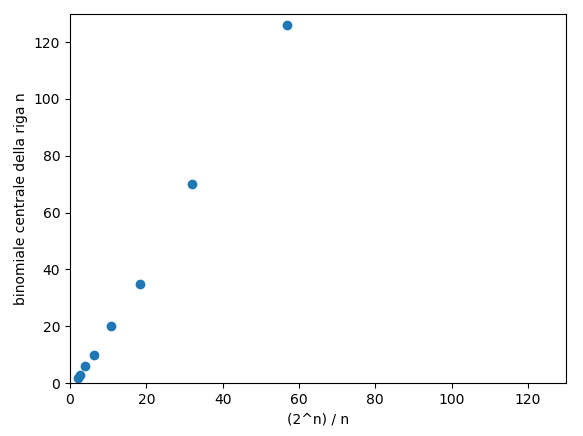
Nell’immagine sottostante si può vedere come la stima data dalla Proprietà N.2 sia abbastanza buona, almeno per i primi valori di n: i binomiali, confrontati con l’espressione \frac{2^n}{n} non assumono valori molto più grandi.
Sempre nell’ottica di minorare i binomiali con delle funzioni più semplici possibili, nel caso di n pari possiamo ottenere una disuguaglianza simile alla (8) ma ancora più semplice, partendo dalla definizione di binomiale piuttosto che dal triangolo di Tartaglia. Prendiamo per esempio il caso di n = 10. Per definizione di binomiale si ha che:
Possiamo riscrivere l’ultima frazione come
Notiamo che l’ultimo termine è 2, mentre gli altri sono tutti maggiori di 2 (infatti la successione dei termini è strettamente decrescente, perché i numeratori decrescono e contemporaneamente i numeratori crescono), perciò
Ricapitolando, abbiamo che
Questa relazione si generalizza facilmente per qualunque n pari, ottenendo che \binom{n}{\frac{n}{2}} \geq 2^{\frac{n}{2}} = \sqrt{2^{n}}:
Minorazione del binomiale centrale del triangolo di Tartaglia, n pari
Per ogni n \geq 2 pari: