La strategia dimostrativa che sarà esposta qui ha come obiettivo la dimostrazione dell’Ipotesi H.1 (Ipotesi di esistenza di coppie di Goldbach basata sui tratteggi) mediante le proprietà degli spazi. Abbiamo individuato due metodi diversi per fare ciò:
- Un metodo che fa uso di una formula per il calcolo esplicito degli spazi;
- Un metodo che fa uso del concetto di massima distanza tra spazi consecutivi.
Entrambi hanno come punto di partenza una riformulazione dell’Ipotesi H.1, diversa in ciascun caso.
Metodo basato sul calcolo esplicito degli spazi
Supponiamo di essere in grado di calcolare esattamente quali sono gli spazi di un tratteggio, con un’espressione algebrica dipendente da una variabile x. L’ideale sarebbe farlo rispettando l’ordine, ossia calcolare una funzione che, dato x, restituisce l’x-esimo spazio. Utilizzando tale funzione, che chiameremo \mathrm{t\_spazio}, è possibile riscrivere i due spazi incogniti p e q dell’Ipotesi H.1 rispettivamente come \mathrm{t\_spazio}(x) e \mathrm{t\_spazio}(y). Si ottiene così la seguente Ipotesi, nella quale le incognite non sono più p e q, ma x e y:
Ipotesi di esistenza di coppie di Goldbach basata sulla funzione \mathrm{t\_spazio}
Siano 2n \gt 4 un numero pari e k il relativo ordine di validità. Allora esistono due interi positivi x e y tali che, con riferimento al tratteggio T_k:
- \mathrm{t\_spazio}(x) e \mathrm{t\_spazio}(y) sono entrambi compresi nell’intervallo di validità;
- \mathrm{t\_spazio}(x) + \mathrm{t\_spazio}(y) = 2n.
Questo metodo, quindi, consiste nel dimostrare che l’equazione \mathrm{t\_spazio}(x) + \mathrm{t\_spazio}(y) = 2n ha almeno una soluzione (x, y), per ogni 2n \gt 4. Chiameremo questa equazione equazione di Goldbach sugli spazi:
Equazione di Goldbach sugli spazi
Siano 2n \gt 4 un numero pari, e k il relativo ordine di validità. Allora la seguente equazione nelle incognite x e y, che si riferisce al tratteggio T_k:
è detta equazione di Goldbach sugli spazi.
La seguente immagine rappresenta graficamente questo metodo risolutivo, sulla base di un esempio:

Come si può intuire, la difficoltà di questo metodo sta nell’esprimere la funzione \mathrm{t\_spazio} mediante un’espressione algebrica, con l’intento che, sostituendo tale espressione nell’equazione di Goldbach sugli spazi, quest’ultima diventi un’equazione algebrica nelle variabili x e y. Ciò ricondurrebbe la ricerca delle soluzioni a un problema di calcolo di tipo algebrico che, in linea di principio, dovrebbe essere affrontabile con diversi strumenti, anche elementari.
Quindi, per giungere all’obiettivo, i passi sarebbero essenzialmente i seguenti:
- Trovare una formula per calcolare la funzione \mathrm{t\_spazio} per tratteggi lineari di ordine qualsiasi (anche se basterebbe trattare il caso dei tratteggi T_k, per qualsiasi k);
- Riscrivere l’equazione di Goldbach sugli spazi, usando la formula trovata;
- Dimostrare che l’equazione così riscritta ha delle soluzioni;
- Dimostrare che, per almeno una delle soluzioni (x, y) individuate, i relativi valori di \mathrm{t\_spazio}(x) e \mathrm{t\_spazio}(y) si trovano nell’intervallo di validità.
Alla fine si potrebbe applicare la Proprietà T.1 (spazi e numeri primi), che ci assicura che tutti gli spazi nell’intervallo di validità sono anche numeri primi, per affermare che le soluzioni così trovate sono anche coppie di Goldbach, il che completerebbe la dimostrazione della congettura.
![]() Calcolo di \mathrm{t\_spazio} per tratteggi di ordine arbitrario
Calcolo di \mathrm{t\_spazio} per tratteggi di ordine arbitrario
Metodo basato sullo studio dei doppi tratteggi
Sarebbe molto più semplice risolvere l’Ipotesi H.1 se, invece di trovare i due spazi p e q, bastasse trovare solo uno dei due, diciamo p. Questo sarebbe possibile se esistesse un meccanismo per garantire che l’intero q = 2n - p sia a sua volta uno spazio, senza porre questa condizione in modo esplicito. Questo meccanismo esiste, ma si basa sull’uso di un tratteggio un po’ più complicato del tratteggio T_k dell’Ipotesi H.1. Vediamo come funziona.
Il principio di base consiste nel limitare le scelte possibili di p, identificando delle condizioni che garantiscano che anche q sia uno spazio. Per trovare queste condizioni, si può partire dalla definizione di spazio. Se q deve essere uno spazio, allora non deve essere divisibile per nessuna componente del tratteggio, che nell’Ipotesi H.1 è T_k. Pertanto q non deve essere divisibile per p_1, \ldots, p_k, ossia q \mathrm{\ mod\ } p_i deve essere diverso da 0, per ogni i=1,\ldots,k. L’aspetto interessante è che questa condizione su q, grazie all’equazione di Goldbach che lega p e q, può essere trasformata in una condizione simile su p. Questo segue da una proprietà generale dei numeri interi, espressa dal seguente Lemma:
Relazione tra i moduli di due interi positivi e quello della loro somma
Siano a, b ed m tre interi positivi. Allora
Indichiamo con a^{\prime}, b^{\prime} ed h^{\prime}, rispettivamente, i quozienti della divisione di a, b ed h per m, per cui a = ma^{\prime} + a \mathrm{\ mod\ } m, b = mb^{\prime} + b \mathrm{\ mod\ } m ed h = mh^{\prime} + h \mathrm{\ mod\ } m. Sostituendo nella (1) si ha che:
Separando i moduli dagli altri termini e mettendo in evidenza m, si ottiene:
Se a \mathrm{\ mod\ } m = 0, si ottiene:
In particolare h \mathrm{\ mod\ } m - b \mathrm{\ mod\ } m è un multiplo di m. Ma h \mathrm{\ mod\ } m e b \mathrm{\ mod\ } m, per definizione di modulo, sono entrambi minori di m, per cui la loro differenza può variare da un minimo di -(m - 1) (quando h \mathrm{\ mod\ } m = 0 e b \mathrm{\ mod\ } m = m - 1) ad un massimo di m - 1 (quando h \mathrm{\ mod\ } m = m - 1 e b \mathrm{\ mod\ } m = 0). Allora l’unico multiplo di m a cui può essere uguale la differenza h \mathrm{\ mod\ } m - b \mathrm{\ mod\ } m è 0, quindi b \mathrm{\ mod\ } m = h \mathrm{\ mod\ } m. Ma h = a + b, per cui b \mathrm{\ mod\ } m = (a + b) \mathrm{\ mod\ } m. Così abbiamo dimostrato l’implicazione verso destra.
Per quanto riguarda l’altra implicazione, supponendo che b \mathrm{\ mod\ } m = (a + b) \mathrm{\ mod\ } m = h \mathrm{\ mod\ } m, sostituendo nella (2) si ottiene:
In particolare a \mathrm{\ mod\ } m è un multiplo di m; ma essendo, per definizione di modulo, compreso tra 0 ed m - 1, non può che essere uguale a zero. Così anche l’implicazione verso sinistra risulta dimostrata.
Applicando il Lemma L.1 nel nostro caso, con a := q, b := p ed m := p_i, e ricordando che p + q = 2n, si ottiene:
Da cui, per negazione, si ottiene:
Questo vale per ogni componente p_i, perché non si è fatta nessuna ipotesi particolare su quale componente scegliere. Ciò significa che la condizione che q sia uno spazio, ossia:
è equivalente alla seguente:
La condizione che q sia uno spazio è stata quindi tradotta in una condizione equivalente su p. In questo modo ci si può concentrare solo sulla singola variabile p.
Tornando all’Ipotesi H.1, bisogna considerare che anche p deve essere uno spazio; quindi, ricapitolando, p deve soddisfare due condizioni:
- Deve essere uno spazio;
- Deve essere tale che anche q = 2n - p sia uno spazio.
La prima condizione si può scrivere come è stato già fatto per q:
La seconda condizione, come si è visto, è data dalla (3). Mettendo insieme le formule (3) e (4), si ottiene la formula seguente:
Si può osservare che p_1 = 2, per cui, nella prima riga, si ha 2n \mathrm{\ mod\ } p_1 = 2n \mathrm{\ mod\ } 2 = 0; quindi l’insieme \{0, 2n \mathrm{\ mod\ } p_1\} è costituito in realtà dal solo numero 0. Si può esplicitare questa condizione separando la prima riga dalle successive, ottenendo:
Per le righe relative a p_2, \ldots, p_k si potrebbe verificare la stessa situazione della prima: per una generica componente p_i, per i = 2, \ldots, k, se p_i fosse uno dei fattori primi di n, 2n \mathrm{\ mod\ } p_i sarebbe 0 e quindi l’insieme \{0, 2n \mathrm{\ mod\ } p_i\} si ridurrebbe al solo elemento 0.
Sulla base dei passaggi sopra esposti si può dimostrare la seguente Proposizione:
Caratterizzazione delle coppie di Goldbach formate da spazi di T_k
Siano 2n \gt 4 un numero pari e k il relativo ordine di validità. Allora, dati due interi positivi p e q, le seguenti condizioni sono equivalenti:
- (p, q) è una coppia di Goldbach per 2n formata da spazi di T_k
- 1 \lt p \lt 2n - 1;
\begin{cases} p \mathrm{\ mod\ } p_1 \neq 0 \\ p \mathrm{\ mod\ } p_2 \notin \{0, 2n \mathrm{\ mod\ } p_2\} \\ \ldots \\ p \mathrm{\ mod\ } p_k \notin \{0, 2n \mathrm{\ mod\ } p_k\} \end{cases}
q = 2n - p.
- 1 \lt p \lt 2n - 1
- \begin{cases} p \mathrm{\ mod\ } p_1 \neq 0 \\ p \mathrm{\ mod\ } p_2 \notin \{0, 2n \mathrm{\ mod\ } p_2\} \\ \ldots \\ p \mathrm{\ mod\ } p_k \notin \{0, 2n \mathrm{\ mod\ } p_k\} \end{cases}
- q = 2n - p
Innanzitutto p non può essere 1, altrimenti non sarebbe primo, quindi non potrebbe formare una coppia di Goldbach. Essendo per ipotesi un intero positivo, deve essere quindi p \gt 1. Lo stesso ragionamento si può ripetere per q, per cui anche q \gt 1. Ma, per l’equazione di Goldbach, p + q = 2n, per cui p = 2n - q, ed essendo q \gt 1 si ha che p \lt 2n - 1. Così abbiamo dimostrato la (a).
Si è visto che la (b) equivale a porre che p e q = 2n - p siano entrambi spazi di T_k, e questo è vero nella 1. dell’enunciato, quindi anche la (b) è dimostrata. Infine la (c) è una scrittura diversa dell’equazione di Goldbach.
Dimostriamo ora il viceversa, 2. \Rightarrow 1. cioè che se valgono (a), (b) e (c), allora (p, q) è una coppia di Goldbach per 2n formata da spazi di T_k, ossia:
- p e q sono spazi di T_k;
- p e q sono primi;
- p + q = 2n.
La (i) segue direttamente dalla (b), come si è visto prima. Per quanto riguarda la (ii), per la Proprietà T.1 (Spazi e numeri primi) basta dimostrare che p e q rientrano nell’intervallo di validità, cioè che p_k + 1 \leq p \leq p_k^2 - 1. Questo è vero perché:
- Il più piccolo spazio di T_k maggiore di 1 è p_k + 1. Infatti, se m è un intero compreso tra 2 e p_k, tutti i suoi fattori primi, essendo minori o uguali ad m, sono minori o uguali a p_k, quindi coincidono con uno dei primi p_1, \ldots, p_k, che sono le componenti di T_k. Quindi m, essendo divisibile per una delle componenti del tratteggio, non è uno spazio. Avendo supposto che 2 \leq m \leq p_k, nessuno di questi m può essere uno spazio, per cui il più piccolo spazio maggiore di 1 è maggiore o uguale a p_k + 1.
- Essendo k l’ordine di validità relativo a 2n, per definizione si ha che 2n \leq p_k^2 - 1; quindi, essendo per la (a) p \lt 2n - 1 \leq 2n, anche p \leq p_k^2 - 1.
Infine, la (iii) segue direttamente dalla (c).
Per capire meglio la formula (5), conviene scomporre le condizioni del tipo p \mathrm{\ mod\ } p_i \notin \{0, 2n \mathrm{\ mod\ } p_i\} nelle due condizioni p \mathrm{\ mod\ } p_i \neq 0 e p \mathrm{\ mod\ } p_i \neq 2n \mathrm{\ mod\ } p_i ed ordinare le condizioni così ottenute come segue:
- p \mathrm{\ mod\ } p_1 \neq 0
- p \mathrm{\ mod\ } p_2 \neq 0
- \ldots
- p \mathrm{\ mod\ } p_k \neq 0
- p \mathrm{\ mod\ } p_2 \neq 2n \mathrm{\ mod\ } p_2
- \ldots
- p \mathrm{\ mod\ } p_k \neq 2n \mathrm{\ mod\ } p_k
Le prime k condizioni dicono che p non deve essere divisibile per p_1, \ldots, p_k, ossia che deve essere uno spazio del tratteggio T_k. A titolo di esempio consideriamo, per k = 4, il tratteggio seguente:
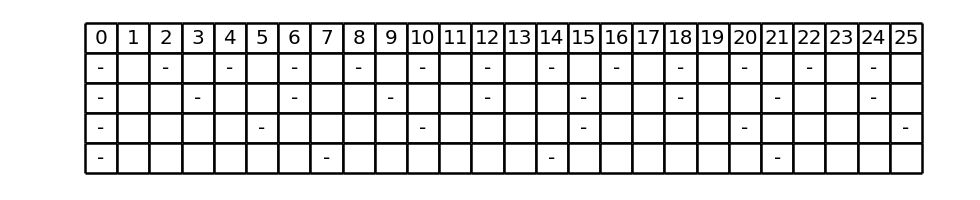
Con riferimento alla rappresentazione di questo tratteggio, i valori di p che soddisfano le prime k condizioni corrispondono alle colonne che non contengono nessun trattino. Infatti su ciascuna riga si riporta un trattino in corrispondenza dei valori di p tali che p \mathrm{\ mod\ } p_i = 0, cioè che non soddisfano la i-esima condizione. Quindi, ragionando al contrario, se la i-esima condizione è soddisfatta, allora la colonna p non contiene un trattino sulla riga i e, ampliando il discorso a tutte le righe, se tutte le prime k condizioni sono soddisfatte, allora la colonna p non contiene nessun trattino, su nessuna riga, ossia per definizione è uno spazio.
Lo stesso ragionamento può essere esteso alle condizioni rimanenti, ovviamente limitandosi ai casi in cui 2n \mathrm{\ mod\ } p_i \neq 0, perché in caso contrario la condizione p \mathrm{\ mod\ } p_i \neq 2n \mathrm{\ mod\ } p_i sarebbe equivalente alla condizione p \mathrm{\ mod\ } p_i \neq 0 già presa in considerazione tra le prime k.
Sia quindi i \in \{2, \ldots, k\} tale che 2n \mathrm{\ mod\ } p_i \neq 0. Consideriamo la condizione p \mathrm{\ mod\ } p_i \neq 2n \mathrm{\ mod\ } p_i. Come abbiamo fatto per le prime k condizioni, possiamo riempire la nostra tabella inserendo un trattino in corrispondenza delle colonne della riga i per cui questa condizione non è soddisfatta, cioè le colonne p tali che p \mathrm{\ mod\ } p_i = 2n \mathrm{\ mod\ } p_i. Nell’espressione 2n \mathrm{\ mod\ } p_i, n è costante, perché è la metà del numero pari del quale cercare le coppie di Goldbach, mentre p_i non è costante in generale, ma lo è sulla riga i. Allora tutta l’espressione 2n \mathrm{\ mod\ } p_i è una costante della riga i, e per semplicità la chiameremo r_i. La condizione p \mathrm{\ mod\ } p_i = 2n \mathrm{\ mod\ } p_i dice che p deve avere questo resto r_i modulo p_i, con r_i \neq 0 per ipotesi. Quindi sulla riga i avremo due successioni di trattini: quella delle colonne con resto 0 modulo p_i e quella delle colonne con resto r_i modulo p_i. I trattini di ciascuna successione sono tra loro equidistanti, ma la loro compresenza sulla stessa riga determina un disegno meno regolare.
Come abbiamo visto nell’Ipotesi H.1, dobbiamo scegliere k come il più piccolo intero tale che (p_{k+1})^2 \gt 100. Ovviamente la funzione (p_{k+1})^2 è crescente rispetto a k, quindi basta provare valori di k crescenti fino a quando il valore della funzione supera 100. Per k = 3 abbiamo che (p_{k+1})^2 = (p_4)^2 = 7^2 = 49 \lt 100, mentre per k = 4 abbiamo (p_{k+1})^2 = (p_5)^2 = 11^2 = 121 \gt 100, per cui il valore di k richiesto è k = 4.
Ora calcoliamo le costanti di riga r_i:
- r_2 = 100 \mathrm{\ mod\ } p_2 = 100 \mathrm{\ mod\ } 3 = 1
- r_3 = 100 \mathrm{\ mod\ } p_3 = 100 \mathrm{\ mod\ } 5 = 0
- r_4 = 100 \mathrm{\ mod\ } p_4 = 100 \mathrm{\ mod\ } 7 = 2
Sostituendo nell’elenco di condizioni che precede la Figura 2, otteniamo:
- p \mathrm{\ mod\ } p_1 \neq 0
- p \mathrm{\ mod\ } p_2 \neq 0
- p \mathrm{\ mod\ } p_3 \neq 0
- p \mathrm{\ mod\ } p_4 \neq 0
- p \mathrm{\ mod\ } p_2 \neq 1
- p \mathrm{\ mod\ } p_4 \neq 2
La condizione p \mathrm{\ mod\ } p_3 \neq 0 è stata scritta solo una volta ma formalmente sarebbe duplicata, perché sostituendo n nella condizione p \mathrm{\ mod\ } p_3 \neq 2n \mathrm{\ mod\ } p_3, essendo 2n \mathrm{\ mod\ } p_3 = r_3 = 0, si ottiene nuovamente la terza condizione.
Nel complesso, inserendo i trattini dove indicato dalla negazione delle prime quattro condizioni si ottiene la precedente Figura 2, mentre considerando anche le ulteriori due condizioni finali si ottiene la seguente Figura (per brevità continuiamo a visualizzare solo la porzione di tabella fino alla colonna 25, mentre per completezza dovremmo arrivare a 100):
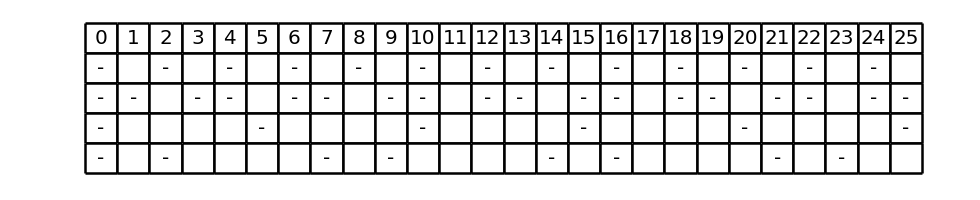
Le colonne di questa nuova Figura che sono prive di trattini rappresentano i valori di p che soddisfano tutte le condizioni del precedente elenco. Ma tali valori di p, se compresi tra 1 e 2n - 1 esclusi, per la Proposizione L.1 sono proprio i valori che fanno parte di una coppia di Goldbach. Ad esempio, un tale p è il numero 11, perché in Figura 3 la colonna 11 non contiene trattini. In effetti, 11 forma proprio una coppia di Goldbach per 100, perché 100 = 11 + 89 e anche 89 è primo. La stessa cosa vale per 17 e le successive colonne prive di trattini che sarebbero visualizzate se prolungassimo la tabella fino a 100: per costruzione, tutte generano coppie di Goldbach (100 = 17 + 83, ecc.).
La Figura 3 rappresenta anch’esso un tratteggio, anche se strutturalmente si presenta in modo molto diverso dalla Figura 2, perché non su tutte le righe i trattini sono tutti equidistanti tra loro. La definizione di tratteggio è abbastanza generale da contemplare entrambi i casi, tuttavia si distinguono diverse tipologie specifiche di tratteggio. I tratteggi rappresentati da tabelle come quella della Figura 2, dove i trattini sono sempre a intervalli regolari e partono da 0, si dicono tratteggi lineari; invece quelli rappresentati da tabella come quella della Figura 3, dove almeno una riga contiene due successioni di trattini equidistanti, una che parte da 0 e l’altra che parte da una costante r_i \neq 0, si chiamano doppi tratteggi (per contrapposizione, a volte i tratteggi lineari sono anche chiamati tratteggi “singoli”). Le nozioni sui doppi tratteggi che bisogna conoscere per comprendere questa strategia dimostrativa saranno introdotte tra poco in questa pagina; è disponibile comunque una pagina di approfondimento dedicata:
Il tratteggio lineare rappresentato dalla Figura 2 si indica, come abbiamo visto, col simbolo T_4, perché le sue componenti sono i primi 4 numeri primi (una notazione alternativa, più esplicita, è quella con l’elenco delle componenti, ossia (2, 3, 5, 7)). Il doppio tratteggio rappresentato dalla Figura 3 si indica invece col simbolo T_4^{(0,1,0,2)}, dove la quadrupla (0,1,0,2) indica, per ciascuna riga, se è presente una successione aggiuntiva di trattini (quando l’elemento della quadrupla è diverso da 0) e, in tal caso, da dove inizia tale sequenza. Ad esempio, in questo caso il secondo elemento della quadrupla è 1 perché sulla seconda riga è presente, rispetto alla Figura 2, la successione di trattini aggiuntiva 1, 4, 7, 10, ecc., dove i trattini sono sempre a intervalli di p_2 = 3 colonne, però partendo da 1 invece che da 0.
In generale, se T è un tratteggio lineare con k righe e (r_1, r_2, \ldots, r_k) è una k-upla di interi non negativi e più piccoli delle corrispondenti componenti del tratteggio, il doppio tratteggio ottenuto partendo da T e aggiungendo, sulle righe i per cui r_i \neq 0, un’ulteriore successione di trattini che inizia da r_i, sarà indicato col simbolo T^{(r_1, r_2, \ldots, r_k)}.
Nel caso della strategia dimostrativa che stiamo descrivendo, come abbiamo visto, i valori di r_i sono dati da 2n \mathrm{\ mod\ } p_i (compreso r_1 che in base a questa formula è sempre 0: spesso, per rendere esplicita questa cosa, scriviamo direttamente 0 al posto di r_1). Quindi possiamo riformulare l’Ipotesi H.1 come segue:
Ipotesi di esistenza di coppie di Goldbach basata sui tratteggi (seconda forma)
Sia 2n \gt 4 un numero pari e sia k il relativo ordine di validità. Sia r_i := 2n \mathrm{\ mod\ } p_i, per ogni i = 2, \ldots, k. Allora il doppio tratteggio T_k^{(0, r_2, \ldots, r_k)} contiene almeno uno spazio p tale che 1 \lt p \lt 2n.
La definizione di doppio tratteggio (che non è necessario conoscere nel dettaglio in questo contesto) include le costanti r_i, ma non è vincolata a un loro particolare valore. Il motivo è che vogliamo affrontare il problema da un punto di vista più generale: se riusciamo a dimostrare l’esistenza di spazi compresi in un certo intervallo (nel nostro caso (1, 2n)) in un doppio tratteggio T^{(r_1, r_2, \ldots, r_k)}, dove T è un qualsiasi tratteggio lineare di partenza e r_1, r_2, \ldots, r_k possono essere qualsiasi, a maggior ragione avremo dimostrato l’esistenza di tali spazi quando T = T_k e r_i = 2n \mathrm{\ mod\ } p_i, che è quanto richiesto dall’Ipotesi H.1 (seconda forma).
Certamente non possiamo aspettarci che tutte le possibili scelte degli r_i generino doppi tratteggi che contengono spazi in un certo intervallo. Ad esempio, se in un doppio tratteggio una componente è 2, cioè tutti i numeri pari sulla riga corrispondente sono trattini, basta porre il corrispondente r_i = 1 per “chiudere” tutti gli spazi rimasti, perché tale scelta implica che anche tutti i numeri dispari sono trattini, quindi non ci sarebbero più spazi né su quella riga, né a maggior ragione in tutto il tratteggio (qualunque siano le eventuali altre componenti e i rispettivi r_i):

Il doppio tratteggio dell’Ipotesi H.1 (seconda forma) ha come prima componente proprio p_1 = 2, ma fortunatamente r_1 = 0, quindi questo problema non si pone; tuttavia il nostro intento è trovare delle condizioni per cui un generico doppio tratteggio T^{(r_1, r_2, \ldots, r_k)} abbia spazi in un determinato intervallo. Ci sono almeno due metodi per fare ciò: essi sono, se vogliamo, dei sotto-metodi di quello basato sullo studio dei doppi tratteggi.
Metodo basato sul calcolo approssimato degli spazi
Il primo metodo si basa sulla seguente osservazione. In fondo noi sappiamo già come è fatto l’intervallo in cui vogliamo cercare spazi, ossia (1, 2n); in particolare, sappiamo che l’estremo inferiore è sempre 1, e che tale estremo è escluso. Quindi, dato un generico doppio tratteggio D, si possono presentare le seguenti possibilità:
- 1 è uno spazio. In tal caso si tratta del primo spazio, dato che 0 sicuramente non lo è. Riprendendo le notazioni iniziali, abbiamo quindi che \mathrm{t\_spazio}_D(1) = 1. Allora, se esistono spazi compresi tra 1 e 2n esclusi, tra di essi ci sarà certamente il secondo. Quindi in questo caso dobbiamo dimostrare che \mathrm{t\_spazio}_D(2) \lt 2n.
- 1 non è uno spazio. In tal caso, se esistono spazi compresi tra 1 e 2n esclusi, tra di essi ci sarà certamente il primo, quindi in questo caso dobbiamo dimostrare che \mathrm{t\_spazio}_D(1) \lt 2n. Riesaminiamo però la condizione del caso precedente: se il secondo spazio fosse minore di 2n, a maggior ragione lo sarebbe anche il primo. Quindi, per dimostrare che \mathrm{t\_spazio}_D(1) \lt 2n, possiamo dimostrare che \mathrm{t\_spazio}_D(2) \lt 2n: in questo caso non è una condizione necessaria, me è sufficiente.
Come abbiamo visto, in qualunque caso la condizione \mathrm{t\_spazio}_D(2) \lt 2n garantirebbe l’esistenza di almeno uno spazio nell’intervallo (1, 2n). Questo, se D è il doppio tratteggio dell’Ipotesi H.1 (seconda forma), garantirebbe la verità dell’Ipotesi stessa, che quindi può essere ulteriormente riformulata:
Ipotesi di esistenza di coppie di Goldbach basata sui tratteggi (terza forma)
Sia 2n \gt 4 un numero pari e sia k il relativo ordine di validità. Sia r_i := 2n \mathrm{\ mod\ } p_i, per ogni i = 2, \ldots, k. Allora il secondo spazio del doppio tratteggio T_k^{(0, r_2, \ldots, r_k)} è minore di 2n.
Questa riformulazione ci riporta al problema iniziale del calcolo degli spazi, questa volta però in un doppio tratteggio invece che in un tratteggio “singolo”. Ma, come abbiamo detto, il calcolo esplicito degli spazi è molto difficile già nei tratteggi singoli, figuriamoci in quelli doppi! Tuttavia, nel nostro caso non dobbiamo calcolare esattamente il secondo spazio, dobbiamo solo dimostrare che è minore di un certo numero fissato; quindi anche un valore approssimato andrebbe bene, purché si riesca a garantire che il valore reale non vi si discosti così tanto da superare 2n. Generalizzando, dato un doppio tratteggio D possiamo fare un ragionamento di questo tipo:
- Supponiamo di trovare una funzione B(x) tale che, per ogni x, \mathrm{t\_spazio}_D(x) \lt B(x)
- Allora, data una costante C, per dimostrare che \mathrm{t\_spazio}_D(x) \lt C basta dimostrare che B(x) \lt C
Il vantaggio, ragionando in tal modo, sarebbe che si può tentare di trovare una funzione B(x) che sia molto più semplice da esprimere algebricamente, rispetto alla funzione \mathrm{t\_spazio}, rendendo semplice il secondo punto. Il problema complicato sarebbe però trovare questa funzione, come richiesto dal primo punto. Abbiamo pensato di trattare questo problema per gradi di difficoltà crescenti, partendo dai tratteggi singoli per ordini crescenti, per poi estendere i risultati ai doppi tratteggi. Al momento abbiamo trovato la funzione B(x) per tratteggi lineari (singoli) fino al quarto ordine (i risultati saranno presto disponibili qui).
Metodo basato sul concetto di massima distanza tra spazi consecutivi
Mentre prima ci siamo focalizzati sull’estremo inferiore dell’intervallo (1, 2n), focalizziamoci ora sulla sua ampiezza. Vedendolo come un intervallo reale, possiamo dire che la sua ampiezza è più piccola di 2n - 1; lo è di una quantità infinitesima, essendo l’intervallo aperto, ma comunque è strettamente minore di 2n - 1. Consideriamo ora gli spazi del doppio tratteggio dell’Ipotesi citata; in particolare consideriamo le coppie di spazi consecutivi: il primo col secondo, il secondo col terzo, e così via. Calcoliamo le differenze (o distanze, termine che preferiamo perché fa pensare alla rappresentazione grafica) tra tali spazi. Avremo quindi infinite distanze: il secondo spazio meno il primo, il terzo meno il secondo, e così via: è una successione infinita di numeri interi. Tale successione è limitata, perché non possono esistere due spazi consecutivi arbitrariamente distanti (ciò deriva dal fatto che i doppi tratteggi, come quelli singoli, sono periodici; quindi, se s è uno spazio, lo è anche s + L, dove L è la lunghezza del periodo, per cui lo spazio successivo ad s non può distare da esso più di L). Ma una successione limitata di numeri interi ammette un massimo, per cui è lecita la seguente Definizione:
Massima distanza tra spazi consecutivi di un tratteggio
Sia T un tratteggio. La massima distanza tra due spazi consecutivi di T sarà indicata col simbolo \mathrm{MDS}(T).
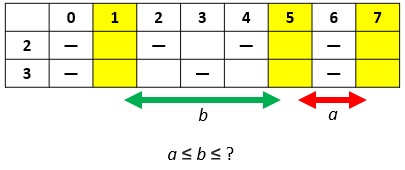
Ora, tornando all’Ipotesi H.1 (seconda forma), supponiamo che \mathrm{MDS}\left(T_k^{(0, r_2, \ldots, r_k)}\right) sia minore di 2n - 1. Allora, se 1 è uno spazio, certamente l’intervallo (1, 2n) conterrebbe un altro spazio del tratteggio, almeno il secondo. Infatti, se il secondo spazio non fosse compreso nell’intervallo, sarebbe maggiore o uguale a 2n, per cui la sua distanza dallo spazio precedente, che è 1, sarebbe almeno 2n - 1, in contrasto con l’ipotesi che \mathrm{MDS}\left(T_k^{(0, r_2, \ldots, r_k)}\right) \lt 2n - 1. Ciò consentirebbe di dimostrare l’Ipotesi H.1 (seconda forma) per tutti i numeri 2n tali che 1 è uno spazio del tratteggio T_k^{(0, r_2, \ldots, r_k)}, ossia è un elemento di una coppia di Goldbach per tale numero; quindi consentirebbe di dimostrarla per tutti i numeri 2n della forma 1 + p, con p primo.
E se 1 non è uno spazio? In tal caso bisogna necessariamente dimostrare che il primo spazio è minore di 2n. Questo può essere fatto in almeno due modi:
- O col metodo precedente, ponendo x = 1 invece che 2.
- Oppure, nel dimostrare che \mathrm{MDS}\left(T_k^{(0, r_2, \ldots, r_k)}\right) \lt 2n - 1, si include anche un teorico “spazio numero 0”. Ciò potrebbe sembrare un artificio, ma se si considerano le espressioni note di \mathrm{t\_spazio}(x) per i tratteggi lineari di primo o di secondo ordine e si prova a valutarle per x = 0, viene fuori che, qualunque sia il tratteggio di partenza, \mathrm{t\_spazio}(0) = -1, per quanto poco intuitivo ciò possa essere. Le formule note per il calcolo della funzione \mathrm{t\_spazio} per i tratteggi lineari sono state ricavate per x \gt 0, ma in fin dei conti sono funzioni matematiche che possono essere valutate anche per altri valori di x, come 0, anche se così facendo ovviamente non calcolano più \mathrm{t\_spazio}, ma qualche funzione più generale che bisognerebbe definire. La stessa cosa potrebbe valere per i doppi tratteggi: magari, dopo aver dimostrato che \mathrm{MDS}\left(T_k^{(0, r_2, \ldots, r_k)}\right) \lt 2n - 1 partendo dalla definizione “classica” di massima distanza, ci si potrebbe accorgere che la stessa dimostrazione varrebbe anche per una definizione “estesa” di massima distanza, in cui la successione delle distanze comincia con la distanza tra il primo spazio e un teorico “spazio numero 0” negativo (sarà -1 come per i tratteggi lineari? La questione è aperta). A questo punto, se la disuguaglianza \mathrm{MDS}\left(T_k^{(0, r_2, \ldots, r_k)}\right) \lt 2n - 1 valesse anche per tale concetto esteso di massima distanza, essendo \mathrm{t\_spazio}(0) negativo, si avrebbe che \mathrm{t\_spazio}(1) \lt \mathrm{t\_spazio}(1) - \mathrm{t\_spazio}(0) \leq \mathrm{MDS}\left(T_k^{(0, r_2, \ldots, r_k)}\right) \lt 2n - 1, per cui \mathrm{t\_spazio}(1) sarebbe minore di 2n, come si vuole dimostrare.
- Anche assumendo che 1 è uno spazio si arriverebbe a un risultato interessante, ossia che esiste una coppia di Goldbach per ogni numero pari della forma 1 + p, con p primo;
- Una conoscenza della massima distanza tra gli spazi consecutivi di un tratteggio sarebbe utile più in generale. Ad esempio, anche solo limitandosi ai tratteggi singoli, dato che nell’intervallo di validità gli spazi coincidono con i numeri primi (Proprietà T.1), si riuscirebbe a dimostrare l’esistenza di un numero primo in un certo intervallo. Sono stati dimostrati diversi teoremi di questo genere, secondo i quali per ogni intero positivo x esiste un numero primo p in un intervallo del tipo (x, C(x) \cdot x), dove C è una funzione che dipende da x. Invece con la presente strategia dimostrativa sarebbe possibile, in linea di principio, dimostrare che esiste un numero primo p in un intervallo del tipo (x, C(x) + x) (cioè si otterrebbe un teorema “additivo” invece che “moltiplicativo”).
Possiamo quindi riformulare l’Ipotesi H.1 (seconda forma) come segue:
Ipotesi di esistenza di coppie di Goldbach basata sulla massima distanza tra spazi
Sia 2n \gt 4 un numero pari e sia k il relativo ordine di validità. Sia r_i := 2n \mathrm{\ mod\ } p_i, per ogni i = 2, \ldots, k. Allora la massima distanza tra due spazi consecutivi del doppio tratteggio T_k^{(0, r_2, \ldots, r_k)} è minore di 2n - 1.
Da un punto di vista generale, siamo interessati a trovare una funzione M tale che, per ogni doppio tratteggio D, \mathrm{MDS}(D) \leq M. Vorremmo trovare in particolare una tale funzione che dipenda solamente dall’ordine di D, ossia dal numero di righe della tabella che lo rappresenta: esisterebbe così una massima distanza M(1) per tutti i doppi tratteggi di primo ordine, una massima distanza M(2) per tutti quelli di secondo, e così via.
A questo proposito, un difetto dell’Ipotesi H.1.MDS è che il numero 2n - 1 dipende da n; sarebbe più conveniente sostituire 2n - 1 con un’espressione che dipende da k, in modo da poter studiare più facilmente cosa succede al variare di k. Questo è possibile ricordando che k è stato definito (Definizione L.2) come il più piccolo intero tale che p_{k+1}^2 \gt 2n. Ciò significa che p_k^2 \leq 2n (altrimenti la relazione che definisce k sarebbe soddisfatta anche da k-1 e quindi verrebbe meno la caratteristica di k di essere il più piccolo intero che la soddisfa), da cui p_k^2 - 1 \leq 2n - 1. Quindi, se si dimostra che la massima distanza tra due spazi consecutivi del doppio tratteggio T_k^{(0, r_2, \ldots, r_k)} è minore di p_k^2 - 1, automaticamente essa sarà anche minore di 2n - 1. Perciò nell’Ipotesi H.1.MDS si può sostituire 2n - 1 con p_k^2 - 1, ottenendo una nuova Ipotesi leggermente più forte, ma più indicata per studiare cosa succede al variare di k:
Ipotesi di esistenza di coppie di Goldbach basata sulla massima distanza tra spazi (versione più forte)
Sia 2n \gt 4 un numero pari e sia k il relativo ordine di validità. Sia r_i := 2n \mathrm{\ mod\ } p_i, per ogni i = 2, \ldots, k. Allora la massima distanza tra due spazi consecutivi del doppio tratteggio T_k^{(0, r_2, \ldots, r_k)} è minore di p_k^2 - 1.
Ricordiamo che le ultime due Ipotesi non implicano sempre l’Ipotesi H.1 (seconda forma), ma lo fanno solo nel caso in cui 1 non è uno spazio (in altri termini, quando tutti gli r_i sono diversi da 1). Tuttavia, come abbiamo visto, questa limitazione ha un’importanza relativa.
Ci sono essenzialmente due approcci per studiare la massima distanza tra due spazi consecutivi di un tratteggio: il calcolo esatto e il calcolo approssimato.
Per quanto riguarda il calcolo esatto, abbiamo sviluppato un programma che fornisce il risultato per qualunque tratteggio o doppio tratteggio lineare (a patto di avere abbastanza tempo a disposizione: il tempo di esecuzione è proporzionale alla lunghezza del periodo del tratteggio).
![]() Calcolatore della massima distanza tra spazi
Calcolatore della massima distanza tra spazi
Per quanto riguarda il calcolo approssimato, lo trattiamo in una pagina dedicata: