Prerequisiti:
Il Teorema di Chen è uno dei teoremi più simili alla Congettura di Goldbach finora noti. Come abbiamo detto in Alcuni risultati importanti – I teoremi di Chen e Yamada, esso è opera del matematico cinese Chen Jingrun, che ne pubblicò la dimostrazione nel 1966. La forma più conosciuta dell’enunciato è la seguente:
Teorema di Chen
Ogni numero pari sufficientemente grande è somma o di due numeri primi, o di un primo e un semiprimo (ossia un prodotto di due numeri primi).
In altri termini, utilizzando le lettere p, q e q^{\prime} per indicare dei numeri primi (non necessariamente distinti), il Teorema ci dice che ogni numero pari N sufficientemente grande si può scrivere o nella forma N = p + q o nella forma N = p + qq^{\prime}. Ci sono quindi due differenze rispetto alla Congettura di Goldbach:
- La validità per numeri “sufficientemente grandi”, invece che per ogni numero pari maggiore di 2
- La presenza del caso N = p + qq^{\prime}
La differenza importante è la seconda, perché lascia il dubbio che esistano alcuni numeri pari che si possano scrivere nella forma N = p + qq^{\prime} ma non nella forma N = p + q, e l’enunciato non dice quanti potrebbero essere. Se si riuscisse a eliminare il caso N = p + qq^{\prime}, e rimanesse così solo la prima differenza, si otterrebbe un enunciato identico alla Congettura a meno del numero “sufficientemente grande” (Ogni numero pari sufficientemente grande è somma di due numeri primi). Tale numero potrebbe essere anche molto grande, anche non noto, ma sarebbe pur sempre un numero finito: resterebbe esclusa dall’enunciato solo una quantità finita di numeri pari, che è ben poco rispetto a tutti gli altri infiniti numeri pari. In termini matematici si direbbe che la forma N = p + q varrebbe per quasi tutti i numeri pari, intendendo tutti eccetto una quantità finita. Perciò possiamo considerare la prima differenza poco significativa nell’ambito dell’infinità dei numeri pari, mentre la vera limitazione del Teorema di Chen è la seconda differenza, ossia la presenza del caso N = p + qq^{\prime}, che invece potrebbe valere per infiniti casi, dato che l’enunciato non dice nulla a riguardo.
Nel nostro sito molto spesso indichiamo il numero pari di partenza della Congettura di Goldbach come 2n, per ricordare che è un numero pari. In questo percorso dedicato al Teorema di Chen lo indicheremo semplicemente con la lettera N. Questo perché utilizzeremo questo numero diverse volte all’interno di espressioni complesse, e se lo indicassimo con 2n le nostre formule sarebbero piene di 2. Perciò in questo percorso bisognerà ricordare che N è sempre pari (quando questo aspetto sarà particolarmente importante, lo ribadiremo).
La forma non abbreviata
Dopo aver analizzato le differenze rispetto alla Congettura di Goldbach, torniamo all’enunciato del Teorema di Chen. Per prima cosa bisogna sapere che quella che abbiamo visto è la forma abbreviata, e più nota, del Teorema. In realtà Chen dimostrò il seguente enunciato più specifico:
Teorema di Chen, versione originale
Sia N un numero pari sufficientemente grande e sia \mathfrak{R}(N) il numero di rappresentazioni di N come somma di un primo dispari e di un prodotto di al più due primi. Allora:
dove
Prima di entrare nel merito dell’enunciato, sono opportune due note sui simboli utilizzati:
-
Il simbolo \gg non è altro che un’alternativa per la notazione “O grande” più comunemente utilizzata; in questo caso però la relazione asintotica di “O grande” deve essere letta a partire dalla funzione che si trova verso la punta del simbolo, per cui la (1) è equivalente a:
\mathfrak{S}(N) \frac{N}{\log^2 N} = O(\mathfrak{R}(N)) -
I simboli \mathfrak{R} e \mathfrak{S} sono le versioni gotiche, o più precisamente Fraktur, rispettivamente delle lettere R e S. Possono essere lette rispettivamente come “R gotico” e “S gotico” e anche queste sono delle notazioni utilizzate di frequente a proposito del Teorema di Chen o di argomenti affini.
Ora entriamo nel merito dell’enunciato. Per prima cosa, esso definisce \mathfrak{R}(N) come il numero di rappresentazioni di N come somma di un primo dispari e di un prodotto di al più due primi. Ciò significa che si stanno considerando tre casi:
- N = p + 1 (un primo più un prodotto di zero primi)
- N = p + q (un primo più un altro primo)
- N = p + qq^{\prime} (un primo più un prodotto di due primi)
Il primo caso viene spesso trascurato perché può verificarsi al massimo una volta (un numero N o è della forma p + 1 o non lo è); gli altri due casi invece possono verificarsi più volte perché c’è più di una variabile in gioco, per cui diversi valori di p possono combinarsi con diversi valori di q e/o q^{\prime}.
Inoltre, come vedremo nel corso della dimostrazione, le somme che rientrano nel conteggio di \mathfrak{R}(N) nel secondo caso sono da considerarsi ordinate, per cui N = q + p è considerata una somma diversa da N = p + q se p \neq q. Il motivo è che in N = p + q si può considerare in alternativa p primo e q prodotto di al più due primi, o viceversa; invece nei casi N = p + 1 e N = p + qq^{\prime} non c’è ambiguità perché 1 e qq^{\prime} non sono primi, quindi il primo può essere solo p. Questo dettaglio comunque non è importante perché, essendo lo scopo dimostrare che esiste almeno una somma, poco importa se essa sia considerata in modo ordinato o no.
Calcoliamo \mathfrak{R}(10) e \mathfrak{R}(12).
Il numero 10 ammette:
- 0 rappresentazioni come 10 = p + 1, perché 9 non è primo;
- 3 rappresentazioni come 10 = p + q, perché 10 = 3 + 7 = 5 + 5 = 7 + 3;
- 0 rappresentazioni come 10 = p + qq^{\prime}, perché p può essere 2, 3, 5 o 7 e in tali casi, rispettivamente, qq^{\prime} dovrebbe essere rispettivamente 8, 7, 5 e 3, ma nessuno di questi numeri è il prodotto di due numeri primi (8 = 2^3 è il prodotto di tre numeri primi, mentre gli altri sono numeri primi, quindi il prodotto di un solo primo).
Quindi \mathfrak{R}(10) = 3.
Il numero 12 ammette:
- 1 rappresentazione come 12 = p + 1, perché 11 è primo;
- 2 rappresentazioni come 12 = p + q, perché 12 = 5 + 7 = 7 + 5;
- 2 rappresentazioni come 12 = p + qq^{\prime}, perché 12 = 2 + 2 \cdot 5 = 3 + 3 \cdot 3, mentre per p = 5, 7, 11 si ottengono i casi precedenti.
Quindi \mathfrak{R}(12) = 5.
È evidente quindi che Chen non solo ha dimostrato che ogni numero pari sufficientemente grande si può scrivere come N = p + q o come N = p + q q^{\prime}, ma ha anche tentato di contare in quanti modi si possa farlo (aggiungendo il caso N = p + 1, che però fa poca differenza, potendo accadere solo una volta). Il conteggio di tali scritture non è però esatto, ma è stimato come ordine asintotico, e la stima è la funzione \mathfrak{S}(N) \frac{N}{\log^2 N}, dove \mathfrak{S}(N) è data dalla (2).
Conviene riscrivere \mathfrak{S}(N) come il prodotto di due fattori:
Analizziamo singolarmente i due fattori:
- Il fattore 2 \prod_{p \gt 2} \left( 1 - \frac{1}{(p - 1)^2} \right) è costante perché, come vedremo in seguito, il prodotto
\begin{aligned}\prod_{p \gt 2} \left( 1 - \frac{1}{(p - 1)^2} \right) & = \\ \left( 1 - \frac{1}{2^2} \right)\left( 1 - \frac{1}{4^2} \right)\left( 1 - \frac{1}{6^2} \right)\left( 1 - \frac{1}{10^2} \right)\ldots & = \\ \frac{3}{4} \frac{15}{16} \frac{35}{36} \frac{99}{100} \ldots \end{aligned}
è convergente, dunque è pari a una certa costante reale (che, per inciso, è la costante dei numeri primi gemelli, che compare nel tentativo di spiegare un’altra famosa congettura).
- Il fattore \prod_{\substack{p \gt 2 \\ p \mid N}} \frac{p - 1}{p - 2} invece dipende da N. Per calcolarlo, in pratica, si moltiplica una frazione del tipo \frac{p - 1}{p - 2} per ogni primo dispari p che divide N. Ad esempio, per N = 18 = 2 \cdot 3^2 questo fattore è uguale a \frac{3 - 1}{3 - 2} = 2 (non si considera né il 2, né la ripetizione del 3), mentre per N = 30 = 2 \cdot 3 \cdot 5 è uguale a \frac{3 - 1}{3 - 2} \frac{5 - 1}{5 - 2}= 2 \cdot \frac{4}{3}.
Il fattore \prod_{\substack{p \gt 2 \\ p \mid N}} \frac{p - 1}{p - 2} che è presente all’interno dell’espressione di \mathfrak{S}(N), e che quindi incide su \mathfrak{R}(N), è un prodotto di frazioni maggiori di 1. Quindi, più divisori primi distinti ha N, più frazioni di questo tipo saranno moltiplicate tra loro, per cui più grande sarà il risultato. Il Teorema di Chen sembra quindi dire che, più fattori primi distinti ha N, più possibili rappresentazioni del tipo N = p + q o N = p + q q^{\prime} esso avrà. Il “sembra” è d’obbligo perché il conteggio delle rappresentazioni è solo stimato come O grande e non calcolato esattamente, tuttavia è interessante notare che la stessa proprietà vale, per i numeri da noi verificabili, per le coppie di Goldbach (quindi considerando solo le somme di tipo p + q). Questa proprietà è più evidente per i cosiddetti “primoriali”, ossia i prodotti dei primi numeri primi: 6 = 2 \cdot 3, 30 = 2 \cdot 3 \cdot 5, 210 = 2 \cdot 3 \cdot 5 \cdot 7, 2310 = 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11, ecc.; infatti questi sono i numeri che hanno più fattori primi distinti rispetto alla grandezza del numero stesso (se ci fossero fattori primi ripetuti, il numero aumenterebbe ma i fattori primi distinti resterebbero gli stessi, diminuendo il rapporto tra numero di fattori primi distinti e grandezza del numero). Per questi numeri, come si può verificare utilizzando il Visualizzatore di coppie di Goldbach, esistono più coppie di Goldbach rispetto ai numeri pari “vicini” (con l’unica eccezione del 6, che è un primoriale ma non ha più coppie di Goldbach rispetto a 4 e 8; tuttavia da 30 in poi la proprietà è sempre verificata e diventa sempre più evidente al crescere dei numeri considerati).
Come si passa dalla forma non abbreviata a quella abbreviata?
Abbiamo detto che il Teorema C.1 è la forma abbreviata del Teorema C.2. Il motivo sta nel fatto che il secondo fattore della (2′) è maggiore di 1, perché prodotto di frazioni maggiori di 1. Questo implica che:
Ma abbiamo detto che l’espressione a destra è una costante, quindi \mathfrak{S}(N) è maggiore di una costante. Con la notazione asintotica possiamo scrivere quindi:
da cui, per la (1):
Quest’ultimo passaggio si giustifica come segue. Per la (1), \mathfrak{R}(N) è definitivamente maggiore di A \cdot \mathfrak{S}(N) \frac{N}{\log^2 N}, con A costante positiva, ma abbiamo detto che anche \mathfrak{S}(N) è maggiore (quindi anche definitivamente maggiore) di un’altra costante positiva, che possiamo chiamare B. Quindi \mathfrak{R}(N) è definitivamente maggiore di A B \frac{N}{\log^2 N}; ossia, essendo il prodotto AB a sua volta costante e positivo, \mathfrak{R}(N) \gg \frac{N}{\log^2 N}.
D’ora in poi, per una questione di brevità ma anche per non annoiare i nostri lettori, non riproporremo più spiegazioni di questo tipo in questo percorso. Se non siete pratici di questo tipo di ragionamenti, prima di proseguire col percorso vi suggeriamo di leggere attentamente l’articolo Proprietà degli ordini asintotici, dove molte proprietà del genere sono dimostrate. Può essere anche utile aver già seguito il percorso sul Teorema dei numeri primi, dove le proprietà degli ordini asintotici vengono applicate frequentemente (specialmente negli ultimi articoli del percorso) e la loro applicazione è spiegata in modo dettagliato.
La relazione (3) significa che \mathfrak{R}(N) è definitivamente maggiore di A \frac{N}{\log^2 N}, dove A è una costante positiva. Ma questa funzione tende a infinito, quindi possiamo scegliere a piacere un intero M ed essere certi che, per N sufficientemente grande, A \frac{N}{\log^2 N} \geq M; quindi, per transitività, anche \mathfrak{R}(N) è maggiore o uguale a M per N sufficientemente grande (ricordiamo che il termine “definitivamente” è equivalente a “per N sufficientemente grande”, è solo più generico). Quindi possiamo porre ad esempio M = 2 ed essere certi che, per N sufficientemente grande, N ammette almeno due rappresentazioni di uno dei tipi citati in precedenza, ossia:
- N = p + 1
- N = p + q
- N = p + qq^{\prime}
Ma abbiamo osservato che il primo caso può presentarsi al massimo una volta; quindi, se ci sono in totale almeno due rappresentazioni di questi tipi, almeno una di esse deve essere del secondo o del terzo tipo. Allora possiamo dire che, per N sufficientemente grande, N ammette almeno una rappresentazione di uno dei due tipi:
- N = p + q
- N = p + qq^{\prime}
che è esattamente quanto asserito dal Teorema C.1.
Il Teorema C.2 quindi implica il Teorema C.1. Possiamo dire che è una versione più forte di esso, perché non si limita a stabilire l’esistenza di una rappresentazione, ma, come abbiamo visto, dice molto in più.
La dimostrazione
Prima di addentrarci nella dimostrazione del Teorema di Chen, cosa che faremo nei prossimi articoli, è bene avere un’idea di cosa ci aspetta. Il primo aspetto da chiarire è che Chen non è partito da zero ma, come spesso accade nella ricerca, si è basato su teoremi già dimostrati da altri matematici prima di lui. Più precisamente, oltre a utilizzare teoremi specifici, si è basato su un’intera teoria matematica, chiamata teoria dei crivelli, che si era sviluppata negli anni precedenti alla sua dimostrazione del 1966. Potremmo rappresentare i principali risultati su cui si è basato Chen come in Figura 1:
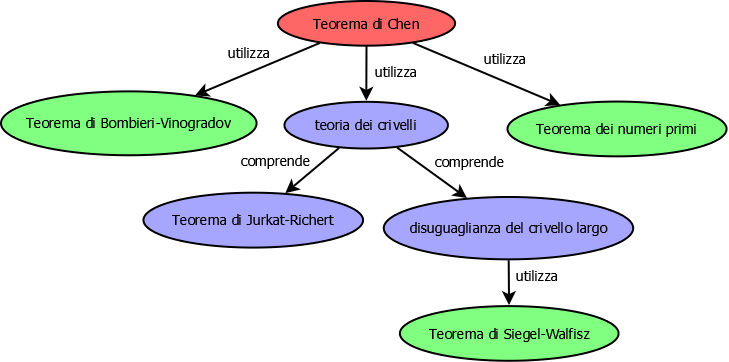
In questo percorso vedremo dettagliatamente la teoria dei crivelli, compresi il Teorema di Jurkat-Richert e la cosiddetta “disuguaglianza del crivello largo”, mentre tratteremo solo l’enunciato del Teorema di Siegel-Walfisz e del Teorema di Bombieri-Vinogradov. Ciascuno di questi ultimi, infatti, richiederebbe un percorso a parte per essere dimostrato, come abbiamo fatto per il Teorema dei numeri primi.
Anche se il Teorema di Chen si basa su teoremi importanti come quelli elencati, ciascuno dei quali ha di per sé una dimostrazione complessa, anch’esso non è da meno: sono necessari infatti molti passaggi logici e algebrici prima di arrivare alla conclusione. Nonostante ciò, ci sono due aspetti positivi della dimostrazione:
- È ben strutturata: il problema iniziale, che consiste nel contare le coppie, viene scomposto in tre sottoproblemi, ciascuno dei quali viene affrontato separatamente, e alla fine le soluzioni dei tre sottoproblemi vengono messe insieme per ottenere la una stima del numero totale di coppie, ossia il Teorema C.2.
- È “elementare”, nel senso che non richiede la conoscenza dell’analisi complessa, riducendo quindi i prerequisiti richiesti per poterla comprendere. Nel nostro sito presupponiamo solamente la conoscenza della matematica scolastica e delle basi di analisi matematica reale, e la dimostrazione del Teorema di Chen si adatta bene a questa scelta.