Il punto di partenza per lo sviluppo della teoria dei tratteggi fu un particolare modo di osservare la successione dei numeri primi:
Se si somma 2 (il primo numero primo) a tutti gli elementi della sequenza, si ottiene
Se si somma 3 (il secondo numero primo) si ottiene
Continuando in questo modo, ed ordinando i risultati ottenuti, si ottiene la seguente tabella, in cui in ogni colonna c’è il valore di ogni somma, in ogni riga c’è il primo addendo, e nella loro intersezione c’è il secondo addendo:
| primo addendo \ somma | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2+ | 2 | 3 | 5 | 7 | 11 | 13 | 17 | ||||||||||||
| 3+ | 2 | 3 | 5 | 7 | 11 | 13 | 17 | ||||||||||||
| 5+ | 2 | 3 | 5 | 7 | 11 | 13 | |||||||||||||
| 7+ | 2 | 3 | 5 | 7 | 11 | 13 | |||||||||||||
| 11+ | 2 | 3 | 5 | 7 | |||||||||||||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
Con riferimento alla Tabella 1, la congettura di Goldbach afferma che le colonne corrispondenti ai numeri pari, dal 4 in poi, non sono mai vuote.
È evidente che una simile proprietà deriva dall'”incastrarsi” della successione dei numeri primi con se stessa, con degli “sfasamenti” che sono i numeri primi stessi e che abbiamo indicato con “2+”, “3+”, “5+”, eccetera. Come dimostrare che in questo complesso gioco di incastri non restano mai “buchi”, cioè colonne vuote, almeno in corrispondenza dei numeri pari maggiori di 2? A Simone non risultava che esistesse una teoria matematica che sia in grado di spiegare nel dettaglio cosa succede in tabelle di questo tipo, a livello di possibili incastri ed in particolare di colonne lasciate vuote. Per rispondere a questa mancanza, egli iniziò lo sviluppo della teoria dei tratteggi.
Non solo le somme di numeri primi, ma anche i numeri primi stessi sono descrivibili mediante tabelle simili alla Tabella 1. Ad esempio possiamo considerare la tabella seguente:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | ||||||||||
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | ||||||||||||||
| 0 | 4 | 8 | 12 | 16 | 20 | |||||||||||||||
| 0 | 5 | 10 | 15 | 20 |
Le differenze rispetto alla Tabella 1 sono le seguenti:
- La successione di interi presente sulle righe non è sempre la stessa: la successione sulla prima riga è (2x)_{x \geq 0} = 0, 2, 4, 6, 8, \dots, sulla seconda riga è (3x)_{x \geq 0} = 0, 3, 6, 9, 12, \dots, eccetera. In generale, la successione degli interi sulla i-esima riga è ((i+1)x)_{x \geq 0};
- Non c’è uno “sfasamento” iniziale che cambia tra una riga e l’altra: in tutte le righe la successione parte col numero 0 nella colonna 0.
In altri termini, mentre nella Tabella 1 la successione degli interi presente su ciascuna riga è sempre la stessa (la successione dei numeri primi), ma ogni riga è sfasata rispetto alla prima di una quantità sempre diversa (un numero primo), nella Tabella 2 ogni riga presenta una successione diversa, ma tutte le successioni hanno il numero 0 nella colonna 0, per cui sono, in questo senso, “sincronizzate” tra loro.
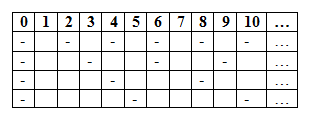
Una conseguenza di questa “sincronizzazione” è che i numeri scritti nelle celle coincidono sempre col numero della colonna dove compaiono, per cui non forniscono nessuna informazione aggiuntiva, rispetto al fatto di esserci (cella contenente un numero) o meno (cella vuota). Essi possono essere quindi sostituiti da un semplice trattino, semplificando la tabella senza perdere alcuna informazione:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| – | – | – | – | – | – | – | – | – | – | – | ||||||||||
| – | – | – | – | – | – | – | ||||||||||||||
| – | – | – | – | – | – | |||||||||||||||
| – | – | – | – | – |
L’aspetto interessante, come accennavamo prima, è che i numeri primi possono essere descritti da tabelle di questo tipo. Infatti, guardando la Tabella 3, sappiamo immediatamente se un dato numero n è divisibile per 2, per 3, per 4 o per 5: basta osservare quali trattini sono presenti nella colonna n. Questa informazione aiuta ad identificare i numeri primi, come preciseremo tra poco, nel paragrafo Tratteggi e numeri primi.
La Tabella 3 è una rappresentazione grafica di un oggetto che chiameremo tratteggio, per come si presentano le righe della tabella. Più precisamente, in questo caso si tratta di un tratteggio lineare, perché la successione dei numeri di colonna dei trattini di ciascuna riga è lineare, ed in particolare del tipo
per qualche intero positivo n fissato (nell’esempio, n = 2, 3, 4, 5). Dato che questo numero n varia tra una riga e l’altra, conviene denotarlo con n_i, dove i varia tra 1 ed il numero di righe della tabella. Così indicheremo con n_1 il numero n associato alla prima riga, con n_2 il numero n associato alla seconda riga, eccetera, per cui nella Tabella 3 si ha che n_1, n_2, n_3, n_4 sono nell’ordine 2, 3, 4, 5. La successione presente sulla riga i diventa allora
Naturalmente ciascuna di queste successioni è infinita, per cui, idealmente, anche le colonne della Tabella 3 dovrebbero essere infinite (sempre partendo da 0). Di fatto si rappresenta, a seconda del contesto, la porzione della tabella che basta per illustrare i concetti che si desidera esprimere, ma resta sottinteso che la tabella dovrebbe avere infinite colonne.
Fissata la legge matematica (2), una tabella come la Tabella 3 è completamente determinata dalle costanti n_1, n_2, \dots, n_k, dove k è il numero di righe della tabella. Queste costanti si dicono componenti del tratteggio; in particolare n_1 è la componente associata alla prima riga, n_2 è la componente associata alla seconda riga, …, in generale n_i è la componente associata alla riga i. Per estensione, diremo anche che i trattini della riga i hanno componente n_i. Indicheremo inoltre il tratteggio con la k-upla (n_1, n_2, \dots, n_k). Quindi la Tabella 3 è la rappresentazione grafica del tratteggio (2, 3, 4, 5). Vedremo in seguito, nell’articolo Tratteggi, trattini e spazi: alcune definizioni e semplici proprietà, la definizione matematica di tratteggio, ma per ora ciò non ha importanza: basti sapere che il tratteggio (2, 3, 4, 5) è l’equivalente, in termini matematici anziché grafici, della Tabella 3.
L’aver scelto una successione lineare del tipo (2), per decidere dove posizionare i trattini della riga i, comporta due conseguenze:
- I trattini di una stessa riga sono equidistanti tra loro, e la loro distanza è pari alla componente associata alla riga;
- La colonna 0 contiene un trattino per ogni riga.
Una cosa importante da notare è che, in una tabella come la Tabella 3, la disposizione generale dei trattini si ripete ogni M colonne, dove M è il minimo comune multiplo delle componenti del tratteggio. Ad esempio, nella Tabella 3, M = \mathrm{MCM}(2, 3, 4, 5) = 60. Infatti 60, essendo il minimo comune multiplo delle componenti, è divisibile per ciascuna di esse, come lo è 0. Quindi la colonna 60 conterrà un trattino per ogni riga, proprio come la colonna 0. Da quella colonna in poi, è facile vedere graficamente (e, volendo, dimostrare) che lo schema del tratteggio si ripete identico: la colonna 61 contiene lo stesso numero di trattini, sulle stesse righe, della colonna 1, e così accade per le altre colonne, come si può vedere confrontando la colonna 62 con la 2, la 63 con la 3, eccetera:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | \dots | 60 | 61 | 62 | 63 | 64 | 65 | \dots |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| – | – | – | – | – | – | – | – | – | – | – | \dots | – | – | – | \dots | |||||||||||||
| – | – | – | – | – | – | – | \dots | – | – | \dots | ||||||||||||||||||
| – | – | – | – | – | – | \dots | – | – | \dots | |||||||||||||||||||
| – | – | – | – | – | \dots | – | – | \dots |
Tratteggi e numeri primi
Vediamo ora come la tabella che rappresenta un tratteggio lineare del tipo (2, 3, \dots n) sia legata ai numeri primi, prendendo come esempio la Tabella 3, che possiamo dividere in tre parti:
- Una parte iniziale, costituita dalle colonne 0 e 1. Sono due colonne speciali perché, per costruzione, la colonna 0 contiene un trattino su ogni riga, mentre la colonna 1, al contrario, non contiene nessun trattino.
- Una parte centrale, costituita dalle colonne 2-5 (in generale 2-n, dove n è la componente più grande del tratteggio).
- Una parte finale, costituita dalle colonne dalla 6 in poi: è tutto ciò che segue la prima e la seconda parte.
Per fissare meglio le idee, evidenziamo queste tre parti con colori diversi:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| – | – | – | – | – | – | – | – | – | – | – | ||||||||||
| – | – | – | – | – | – | – | ||||||||||||||
| – | – | – | – | – | – | |||||||||||||||
| – | – | – | – | – |
Analizzando la parte centrale e la parte finale dal punto di vista dei numeri primi, si può notare che:
- Nella parte centrale (gialla), tutte e sole le colonne che contengono un solo trattino sono numeri primi;
- Nella parte finale (verde), tutte e sole le colonne che non contengono trattini sono numeri primi.
Entrambe le proprietà derivano dal fatto che i numeri primi sono divisibili solo per se stessi e per 1. Perciò nella rappresentazione di un tratteggio lineare del tipo (2, 3, \dots, n), nella colonna di un numero primo p può esserci al massimo un trattino, sulla riga di componente p, se p è una componente del tratteggio (il divisore 1 non si considera perché 1 non è una componente del tratteggio: questo sarebbe il caso degenere che abbiamo escluso). Ma p è una componente del tratteggio (2, 3, ..., n) solo se p \leq n, cioè solo se la colonna appartiene alla parte centrale. Questo ragionamento spiega che:
- Nella parte centrale (gialla), tutte le colonne dei numeri primi contengono un solo trattino;
- Nella parte finale (verde), tutte le colonne dei numeri primi non contengono trattini.
Per quanto riguarda il viceversa, se la colonna p contiene un solo trattino, vuol dire che p è divisibile per una sola componente del tratteggio, cioè per un solo numero dell’insieme \{2, 3, \dots, n\}. Ma questo comporta che p sia primo? Dipende:
- Se la colonna di p appartiene alla parte centrale, che per definizione comprende le colonne coi numeri delle componenti del tratteggio, allora p è una componente del tratteggio. Essendo p ovviamente divisibile per se stesso, ci sarà un trattino (chiamiamolo t) all’incrocio tra la riga di componente p e la colonna p. Ma abbiamo ipotizzato che la colonna p contiene un solo trattino, che quindi deve essere proprio t. Allora l’unico trattino della colonna p si trova sulla riga relativa alla componente p: ciò significa che p non è divisibile per le altre componenti del tratteggio. Le componenti sono 2, 3, \dots, n e tra di esse vi è p, dunque p non è divisibile per nessun altro numero compreso tra 2 e p, cioè è primo.
- Nella parte finale, il viceversa è verificato nella Tabella 5, perché l’ultima colonna considerata è la numero 20, ma non lo sarebbe se ci fossero abbastanza colonne. Infatti, se un numero non è divisibile per 2, 3, 4 e 5 non significa che sia primo, perché potrebbe essere il prodotto di numeri primi più grandi di 5. Il più piccolo numero del genere è 7 \cdot 7 = 49, prodotto di due primi maggiori di 5 e più piccoli possibile. La Tabella 6 visualizza graficamente questa proprietà.
| \dots | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | \dots |
|---|---|---|---|---|---|---|---|---|---|---|---|
| \dots | – | – | – | – | – | \dots | |||||
| \dots | – | – | – | \dots | |||||||
| \dots | – | – | \dots | ||||||||
| \dots | – | – | \dots |
Nella rappresentazione di un tratteggio, le colonne che non contengono trattini sono dette spazi. Per estensione, sono detti spazi anche i numeri associati a tali colonne. Ad esempio, con riferimento alla Tabella 6, 49 è un esempio di uno spazio che non è un numero primo.
Generalizzando il ragionamento precedente, ed introducendo il concetto di spazio, possiamo enunciare la seguente proprietà:
Spazi e numeri primi
Nella rappresentazione del tratteggio lineare (2, 3, \dots, n):
- Tutte le colonne comprese tra 2 ed n sono numeri primi se e solo se contengono un solo trattino;
- Tutte le colonne comprese tra n + 1 e p^2 - 1, dove p è il più piccolo numero primo maggiore di n, sono numeri primi se e solo se sono spazi;
- Tutte le colonne da p^2 in poi che sono primi, sono anche spazi; ma esistono spazi che non sono primi (il più piccolo dei quali è p^2).
Gli spazi sono dunque un concetto importante, perché permettono di caratterizzare i numeri primi compresi tra n + 1 e p^2 - 1 (secondo punto della Proprietà T.1). Per semplificare, possiamo restringere questo intervallo togliendo il riferimento a p; infatti p è il più piccolo numero primo maggiore di n e dunque n + 1 \leq p, da cui (n+1)^2 - 1 \leq p^2 - 1. Perciò possiamo dire che gli spazi del tratteggio (2, 3, \dots, n) permettono di caratterizzare almeno i numeri primi compresi tra n + 1 e (n+1)^2 - 1 = n^2 + 2n. Per n = 2, 3, \dots si ottengono i seguenti intervalli:
- per n = 2, da 3 a 8;
- per n = 3, da 4 a 15;
- per n = 4, da 5 a 24;
- per n = 5, da 6 a 35;
- per n = 6, da 7 a 48.
- …
Possiamo dire quindi che il tratteggio (2, 3, \dots, n) ci consente di ottenere un’esatta descrizione di una porzione dei numeri primi, la cui lunghezza aumenta quadraticamente con n, ed avente un minimo che aumenta linearmente con n. Su questa proprietà si basa lo studio dei numeri primi attraverso la teoria dei tratteggi.
I numeri naturali, che sono le colonne della tabella che rappresenta il tratteggio (2, 3, \dots, n), possono essere partizionati in due sottoinsiemi: quelli che non sono divisibili per nessuna componente del tratteggio, ossia gli spazi, e quelli che sono divisibili per almeno una componente (non importa per quante componenti). Osserviamo che questa distinzione resterebbe inalterata se eliminassimo dal tratteggio le componenti che sono multiple di altre. Ad esempio, se dal tratteggio (2, 3, 4, 5) togliessimo la componente 4, perché 4 è multiplo di 2, otterremmo il tratteggio (2, 3, 5) rappresentato dalla tabella seguente:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| – | – | – | – | – | – | – | – | – | – | – | ||||||||||
| – | – | – | – | – | – | – | ||||||||||||||
| – | – | – | – | – |
Questa tabella ha gli stessi spazi della Tabella 3: 1, 7, 11, 13, 17, 19 (dove 7, …, 19 sono i primi compresi tra 6 e 20, applicando la Proprietà T.1 e considerando che l’ultima colonna della tabella, 20, è minore di 7^2 = 49, dove 7 è il più piccolo primo maggiore di 5). Per capire perché, pensiamo a cosa succede quando si aggiunge una riga ad un tratteggio lineare. Ad esempio potremmo ottenere il tratteggio (2, 3, 5) rappresentato nella Tabella 7 partendo dal tratteggio (2, 3) ed aggiungere la componente 5:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| – | – | – | – | – | – | – | – | – | – | – | ||||||||||
| – | – | – | – | – | – | – | ||||||||||||||
| – | – | – | – | – |
Su 20 colonne, abbiamo aggiunto 5 trattini in totale, nelle colonne 0, 5, 10, 15 e 20. Tranne quello della colonna 5, vediamo che tutti gli altri si trovano in colonne già occupate da altri trattini: ad esempio la colonna del 10, prima dell’aggiunta della nuova riga, aveva già un trattino di componente 2, perché 10 è divisibile per 2. La colonna 5, invece, non aveva trattini nel tratteggio (2, 3), quindi 5 era uno spazio prima dell’aggiunta della riga e non lo è dopo.
In generale, aggiungendo una riga ad un tratteggio, gli spazi precedenti possono rimanere (come 7 o 11, nella Tabella 8) o scomparire (come 5). Tuttavia, se in particolare la componente che aggiungiamo al tratteggio è multipla di altre già esistenti, gli spazi rimangono tutti. Un esempio è quando si passa dal tratteggio (2, 3, 5) al tratteggio (2, 3, 4, 5), essendo 4 multiplo di 2:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| – | – | – | – | – | – | – | – | – | – | – | ||||||||||
| – | – | – | – | – | – | – | ||||||||||||||
| – | – | – | – | – | – | |||||||||||||||
| – | – | – | – | – |
In questo caso tutti i trattini aggiunti con la riga di componente 4 si posizionano in colonne già occupate da altri trattini, in particolare da trattini di componente 2, per il semplice fatto che un numero divisibile per 4 è divisibile anche per 2. Dunque i trattini introdotti con la riga di componente 4 non vanno a “riempire” nessuno spazio di (2, 3, 5), per cui i tratteggi (2, 3, 5) e (2, 3, 4, 5) hanno gli stessi spazi.
Generalizzando questo ragionamento, si ottiene la seguente proprietà:
Tratteggi che hanno gli stessi spazi
Siano n \geq 2 un intero e p_i l’i-esimo numero primo: p_1 = 2, p_2 = 3, p_3 = 5, \dots. I tratteggi (2, 3, \dots, n) e (p_1, p_2, \dots, p_k), dove p_k è il più grande numero primo minore o uguale ad n, hanno gli stessi spazi.
Più in generale, il tratteggio (n_1, n_2, \dots, n_j) ha gli stessi spazi del tratteggio che ha per componenti l’insieme ottenuto partendo da \{n_1, n_2, \dots, n_j\}, rimuovendo tutte le componenti che sono multiple di altre.
Osserviamo che, attraverso l’operazione di aggiunta di una riga ad un tratteggio lineare, possiamo ottenere il tratteggio (2, 3, \dots, n) con i seguenti passaggi:
dove la freccia indica l’aggiunta di una riga. Inoltre, per la Proprietà T.2, potremmo togliere i passaggi dove si aggiunge una componente multipla di altre già aggiunte, mantenendo gli spazi nel risultato finale.
Questo procedimento è la trasposizione, nei concetti della teoria dei tratteggi, del noto crivello di Eratostene, mediante il quale si ottiene l’insieme dei numeri primi fino a un certo n. La differenza è che nel crivello, in termini di teoria dei tratteggi, su ciascuna riga aggiunta non si riporta il primo trattino dopo la colonna 0. Ad esempio, fermandosi a 4 iterazioni del crivello, cioè fermandosi alla quarta riga, si ottiene la seguente tabella:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| – | – | – | – | – | – | – | – | – | – | |||||||||||
| – | – | – | – | – | – | |||||||||||||||
| – | – | – | – | – | ||||||||||||||||
| – | – | – | – |
In questo modo si ottiene la completa identificazione tra spazi e numeri primi, diversamente da quanto asserito dalla Proprietà T.1 per i tratteggi lineari. Il tratteggio rappresentato nella Tabella 10 non è però lineare. Sarebbe forse più facile studiare i numeri primi partendo da tratteggi non lineari tipo quello mostrato nella Tabella 10 ma, d’altra parte, i tratteggi lineari hanno il vantaggio di poter essere descritti da formule semplici e, nello scegliere un modello di partenza, molte volte è meglio preferire la semplicità piuttosto che l’accuratezza nella rappresentazione della realtà (in questo caso la realtà rappresentata è la successione dei numeri primi). I tratteggi lineari in questo senso sono un buon compromesso, in quanto costituiscono un modello semplice ma comunque abbastanza accurato, nel senso precisato dalla Proprietà T.1.