Prerequisiti:
Nell’articolo precedente abbiamo definito in cosa consiste il problema del downcast, la cui risoluzione permette di calcolare le funzioni \mathrm{t}, \mathrm{t\_valore} e \mathrm{t\_spazio} per tratteggi di ordine arbitrario. In questo articolo vedremo che, nell’ipotesi che i tratteggi coinvolti siano lineari, risolvere il problema del downcast significa trovare la soluzione di particolari equazioni, dette equazioni caratteristiche del downcast. In questo articolo vedremo le equazioni caratteristiche che permettono di risolvere il problema del downcast di \mathrm{t} e di \mathrm{t\_valore}, mentre successivamente vedremo quelle che valgono per la funzione \mathrm{t\_spazio}.
L’ipotesi di linearità dei tratteggi è molto importante. Per capire perché, consideriamo la formulazione del problema del downcast (Definizione T.10 (Funzione di downcast)):
Sebbene questa definizione valga per qualunque tipo di tratteggio, quando si tenta di tradurre in formule l’equazione f_T(x) = f_U(y) bisogna conoscere esattamente le espressioni delle funzioni f_T ed f_U (dove f può essere \mathrm{t}, \mathrm{t\_valore} o \mathrm{t\_spazio}), e queste dipendono dal tipo di tratteggio. Proseguiremo quindi con l’ipotesi di trattare sempre tratteggi lineari.
In linea di principio si potrebbe tentare di risolvere il problema del downcast anche per tratteggi non lineari, ma la teoria dei tratteggi non tratta ancora questo tema. Un altro punto aperto è cercare proprietà del downcast che valgono per qualsiasi tratteggio, o per classi di tratteggi più ampie di quelli lineari.
Equazioni caratteristiche generali del downcast di \mathrm{t} lineare
Affrontiamo ora più nel dettaglio il problema del downcast di \mathrm{t} da un tratteggio T ad un suo sottotratteggio U (ricordiamo che una funzione di downcast di \mathrm{t} è anche una funzione di downcast di \mathrm{t\_valore}, perciò parliamo solo di \mathrm{t}).
Fissiamo un certo ordinale x e chiamiamo t l’x-esimo trattino di T. Supponiamo che t \in U (in modo che il downcast sia possibile) e chiamiamo y il suo ordinale in U. Allora, come abbiamo visto nell’articolo Il problema del downcast, una funzione di downcast di \mathrm{t} da T ad U associa al numero x il numero y. Per ottenere questa funzione, dobbiamo capire innanzitutto come solo legati tra loro x ed y. Come dicevamo inizialmente, questo legame consiste in un’equazione, detta equazione caratteristica del downcast. In realtà non esiste una sola equazione caratteristica, me ne esistono diverse, che variano per la forma in cui sono scritte, o per le assunzioni che si fanno su T ed U. Le più generali sono espresse nella seguente Proposizione:
Equazioni caratteristiche generali del downcast di \mathrm{t}, per tratteggi lineari
Sia T) un tratteggio lineare ed U un suo sottotratteggio. Sia t un trattino di entrambi, avente ordinale x in T ed y in U. Sia i l’indice della riga di t. Allora vale l’uguaglianza:
x = y + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \lt i} \left \lfloor \frac{\mathrm{t\_valore}_U(y)}{n_{i^{\prime}}} \right \rfloor + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \gt i} \left \lfloor \frac{\mathrm{t\_valore}_U(y) - 1}{n_{i^{\prime}}} \right \rfloor \tag{4}Oppure, equivalentemente:
x = y + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U} \left \lfloor \frac{\mathrm{t\_valore}_U(y) - (i^{\prime} \gt i)}{n_{i^{\prime}}} \right \rfloor \tag{4$^{\prime}$}In particolare, se U è di primo ordine (U = T[i]), vale l’uguaglianza
x = y + \sum_{i^{\prime} \lt i} \left \lfloor \frac{n_i y}{n_{i^{\prime}}} \right \rfloor + \sum_{i^{\prime} \gt i} \left \lfloor \frac{n_i y - 1}{n_{i^{\prime}}} \right \rfloor \tag{6}Oppure, equivalentemente:
x = y + \sum_{i^{\prime} \neq i} \left \lfloor \frac{n_i y - (i^{\prime} \gt i)}{n_{i^{\prime}}} \right \rfloor \tag{6$^{\prime}$}In questa Proposizione abbiamo due coppie di equazioni caratteristiche: (4) e (4′), (6) e (6′). La prima coppia è quella più generica, valida qualunque siano T ed U, mentre le equazioni della seconda coppia valgono solo nel caso in cui U sia di primo ordine (per quanto riguarda T non si fa nessuna ipotesi sull’ordine in nessuna delle due coppie). All’interno di ciascuna coppia, le due equazioni differiscono tra loro solo per la forma in cui sono scritte: quelle con l’apice, (4′) e (6′), sono una forma compatta di quelle senza apice, rispettivamente (4) e (6), e usano la notazione abbreviata (i^{\prime} \gt i), che vale 1 se la condizione tra parentesi è verificata e 0 altrimenti.
Ad esempio il numeratore della frazione nella (6′), n_i y - (i^{\prime} \gt i), vale n_i y se i^{\prime} \le i, n_i y - 1 se i^{\prime} \gt i, per cui si vede facilmente che la (6′) è equivalente alla (6); un analogo discorso vale anche per le formule (4) e (4′).
Osserviamo che, se U è di primo ordine, deve essere necessariamente U = T[i], come riporta l’enunciato della Proposizione. Infatti il sottotratteggio U contiene il trattino t e quindi deve contenere la sua riga, che ha indice i, cioè deve contenere T[i]. Ma allora, dato che abbiamo supposto che sia di primo ordine, deve essere proprio uguale a T[i].
Infine, osserviamo che nelle formule (4′) e (6′) gli indici delle sommatorie variano tra gli indici delle righe di T che non appartengono ad U (per quanto riguarda la (6) si deve tener conto che U = T[i]). Per le formule (4) e (6) vale sostanzialmente la stessa cosa, con la differenza che la sommatoria è spezzata in due parti; in ogni caso però, in corrispondenza di ogni indice di sommatoria, si ha un termine con la parte intera. Allora il numero di termini con la parte intera, una volta che le sommatorie sono state espanse, è sempre uguale al numero delle righe di T che non stanno in U, ossia all’ordine di T meno l’ordine di U. In pratica, il numero di parti intere ci dice di quanti ordini scendiamo quando facciamo il downcast da T ad U: nel paragrafo seguente vedremo alcuni esempi.
Ma cosa rappresentano questi termini con la parte intera? Essi non sono altro che dei conteggi di trattini su una singola riga, ottenuti applicando la Proposizione T.2 (Conteggio dei trattini fino a un certo valore in un tratteggio lineare di primo ordine) ed il suo Corollario (si vedano i dettagli seguenti per un approfondimento).
Abbiamo detto che x è l’ordinale di t in T, quindi in T esistono x trattini minori o uguali a t. Possiamo chiamare X questo insieme di trattini e partizionarlo in due sottoinsiemi, a seconda dell’appartenenza dei trattini ad U:
- Insieme Y: trattini di U minori o uguali a t
- Insieme \bcancel{Y}: trattini di T che non appartengono ad U, minori di t (se un trattino non appartiene ad U non può essere uguale a t, perché t \in U)
Abbiamo chiamato Y il primo sottoinsieme perché contiene esattamente y trattini. Infatti dire che t è l’y-esimo trattino di U equivale a dire che in U ci sono y trattini minori o uguali a t, che costituiscono appunto l’insieme Y.
Analogamente, possiamo chiederci quanti elementi contiene l’altro sottoinsieme, \bcancel{Y}. La strategia che adotteremo per contarli è quella di dividerli per righe, contarli riga per riga e poi sommare il tutto. A questo proposito bisogna osservare che il conteggio dei trattini su una riga dipende dalla posizione della riga stessa rispetto a quella di t. Infatti, per la Definizione T.4 (Ordinamento di trattini), i trattini minori o uguali a t sono quelli che hanno valore minore del valore di t oppure, tra quelli con lo stesso valore, quelli che appartengono ad una riga con indice più piccolo. Quindi, per contare i trattini di \bcancel{Y} per righe, posto che t si trova sulla riga i, bisogna procedere in questo modo:
- Sulle righe che hanno indice minore di i (righe verdi nella Figura 1), vanno contati tutti i trattini aventi valore minore o uguale al valore di t, che chiamiamo v. Possiamo chiamare questo insieme di trattini \bcancel{Y}_- (dove il – sta per “indice minore”).
- Sulle righe che hanno indice maggiore di i (righe rosse nella Figura 1), vanno contati tutti i trattini aventi valore minore di v. Possiamo chiamare questo insieme di trattini \bcancel{Y}_+ (dove il + sta per “indice maggiore”).
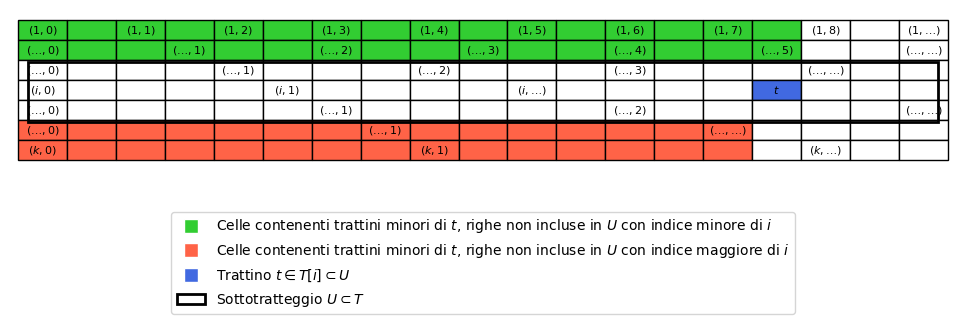
Ora, grazie alla Proposizione T.2 (Conteggio dei trattini fino a un certo valore in un tratteggio lineare di primo ordine) ed al suo Corollario, possiamo contare gli elementi degli insiemi \bcancel{Y}_- ed \bcancel{Y}_+. L’insieme \bcancel{Y}_- contiene, per la Proposizione T.2, \left \lfloor \frac{v}{n_{i^{\prime}}} \right \rfloor trattini per ogni riga non inclusa in U avente indice i^{\prime} \lt i. Quindi in totale si ha:
|\bcancel{Y}_-| = \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \lt i} \left \lfloor \frac{v}{n_{i^{\prime}}} \right \rfloor \tag{1}L’insieme \bcancel{Y}_+ invece contiene, per il Corollario della Proposizione T.2, \left \lfloor \frac{v - 1}{n_{i^{\prime}}} \right \rfloor trattini per ogni riga non inclusa in U avente indice i^{\prime} \gt i. Quindi in totale si ha:
|\bcancel{Y}_+| = \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \gt i} \left \lfloor \frac{v - 1}{n_{i^{\prime}}} \right \rfloor \tag{2}Ora non resta che ricomporre i vari elementi per ottenere un’equazione che lega x ed y:
- L’insieme X dei trattini di T minori o uguali a t contiene x elementi e si partiziona nel due sottoinsiemi Y e \bcancel{Y}
- Il sottoinsieme Y contiene y elementi
- Il sottoinsieme \bcancel{Y} si partiziona ulteriormente in \bcancel{Y}_- ed \bcancel{Y}_+, il cui numero di elementi è dato rispettivamente dalle formule (1) e (2)
Allora
\begin{aligned} x &= |X| \\&= |Y| + |\bcancel{Y}| \\&= |Y| + |\bcancel{Y}_-| + |\bcancel{Y}_+| \\&= y + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \lt i} \left \lfloor \frac{v}{n_{i^{\prime}}} \right \rfloor + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \gt i} \left \lfloor \frac{v - 1}{n_{i^{\prime}}} \right \rfloor \end{aligned}Quindi
x = y + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \lt i} \left \lfloor \frac{v}{n_{i^{\prime}}} \right \rfloor + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \gt i} \left \lfloor \frac{v - 1}{n_{i^{\prime}}} \right \rfloor \tag{3}Abbiamo ottenuto un’equazione che lega x ed y, che è ciò che cercavamo. Quest’equazione però non consente ancora di calcolare y (e quindi di risolvere il problema del downcast), perché contiene ancora le incognite v ed i, ossia il valore e l’indice di riga di t. Tuttavia, i non è una vera incognita, perché si può calcolare applicando alcuni teoremi, come vedremo nei prossimi articoli. Ipotizzando di applicare questi teoremi possiamo ritenere i già nota, ed occuparci solo di v. Questa, diversamente da i, è una vera incognita, anche perché, se oltre ad i conoscessimo anche v, potremmo calcolare direttamente t = (i, \frac{v}{n_i}) e quindi verrebbe meno l’utilità del downcast, il cui scopo è proprio il calcolo del trattino t. Quindi, se vogliamo risolvere il problema del downcast, dobbiamo in qualche modo eliminare l’incognita v dall’equazione (3). Un modo per farlo è esprimere questa incognita in funzione delle altre già presenti. In particolare, è possibile esprimere v in funzione di y; infatti, essendo v il valore di t, che è l’y-esimo trattino di U, si ha che v = \mathrm{t\_valore}_U(y). Sostituendo questo nella (3) abbiamo:
x = y + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \lt i} \left \lfloor \frac{\mathrm{t\_valore}_U(y)}{n_{i^{\prime}}} \right \rfloor + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \gt i} \left \lfloor \frac{\mathrm{t\_valore}_U(y) - 1}{n_{i^{\prime}}} \right \rfloor \tag{4}Possiamo esprimere quest’equazione in una forma più compatta utilizzando la Definizione T.12, con C := i^{\prime} \gt i:
x = y + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \neq i} \left \lfloor \frac{\mathrm{t\_valore}_U(y) - (i^{\prime} \gt i)}{n_{i^{\prime}}} \right \rfloorOra le due sommatorie della (4), una per gli indici maggiori di i ed una per quelli minori (sempre tra gli indici che non sono considerati in U), sono state riunite in una sola, che vale per tutti gli indici, sia quelli minori che quelli maggiori.
Notiamo che così facendo la condizione i^{\prime} \neq i è diventata superflua, perché se T[i^{\prime}] \nsubseteq U allora i^{\prime} non è nessuno degli indici di riga di U, quindi nemmeno i. Allora la formula precedente si riscrive più semplicemente come segue:
Esiste un caso particolare in cui le equazioni (4) e (4′) assumono una forma particolarmente semplice: è quando il sottotratteggio U è di primo ordine. Ciò, come abbiamo già osservato, equivale a dire che U = T[i]. In questo caso, essendo t l’y-esimo trattino di U, il suo valore deve essere v = n_i y. Sostituendo questo nella (4), si ha
x = y + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \lt i} \left \lfloor \frac{n_i y}{n_{i^{\prime}}} \right \rfloor + \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U,\ i^{\prime} \gt i} \left \lfloor \frac{n_i y - 1}{n_{i^{\prime}}} \right \rfloor \tag{5}Ora le condizioni T[i^{\prime}] \nsubseteq U,\ i^{\prime} \lt i e T[i^{\prime}] \nsubseteq U,\ i^{\prime} \gt i si possono semplificare, perché essendo U = T[i] si ha che T[i^{\prime}] \nsubseteq U \Leftrightarrow T[i^{\prime}] \nsubseteq T[i] \Leftrightarrow i^{\prime} \neq i, ma quest’ultima condizione è superflua perché già compresa nelle condizioni i^{\prime} \lt i e i^{\prime} \gt i, quindi la (5) diventa semplicemente:
x = y + \sum_{i^{\prime} \lt i} \left \lfloor \frac{n_i y}{n_{i^{\prime}}} \right \rfloor + \sum_{i^{\prime} \gt i} \left \lfloor \frac{n_i y - 1}{n_{i^{\prime}}} \right \rfloor \tag{6}Oppure, in forma più compatta:
x = y + \sum_{i^{\prime} \neq i} \left \lfloor \frac{n_i y - (i \lt i^{\prime})}{n_{i^{\prime}}} \right \rfloor \tag{6$^{\prime}$}Equazioni caratteristiche del downcast di \mathrm{t} lineare: casi particolari
Vediamo ora alcuni casi particolari delle equazioni caratteristiche generali del downcast, che compaiono nell’enunciato della Proposizione T.4.
Cominciamo dal caso in cui T ha ordine 2. In questo caso il sottotratteggio U non può che essere di primo ordine (a meno che si voglia considerare il sottotratteggio improprio U = T, ma in questo caso il downcast è banale perché sarebbe x = y). Allora possiamo partire dalle formule (6) e (6′), specifiche per questo caso. Per quanto riguarda la formula (6), consideriamo separatamente i casi i = 1 ed i = 2:
- Se i = 1, non esistono indici i^{\prime} \lt i, perciò la prima sommatoria è vuota, mentre nella seconda l’unico valore possibile di i^{\prime} è 2;
- Se i = 2, non esistono indici i^{\prime} \gt i, perciò la seconda sommatoria è vuota, mentre nella prima l’unico valore possibile di i^{\prime} è 1.
Quindi l’equazione (6) diventa:
- Per i = 1: x = y + \left \lfloor \frac{n_1 y - 1}{n_2} \right \rfloor
- Per i = 2: x = y + \left \lfloor \frac{n_2 y}{n_1} \right \rfloor
Se invece partiamo dalla formula (6′), otteniamo la forma compatta x = y + \left \lfloor \frac{n_i y - (j \gt i)}{n_j} \right \rfloor, dove j è l’unico indice diverso da i: j = 2 se i = 1 e, viceversa, j = 1 se i = 2. Possiamo esprimere questo vincolo tra i e j con l’espressione \{i, j\} = \{1, 2\}. Così infatti diciamo che i e j, presi insieme, devono formare l’insieme \{1, 2\}, quindi:
- se i = 1, per poter formare l’insieme \{1, 2\}, j deve essere 2
- se i = 2, per lo stesso motivo j deve essere 1
Allora per i tratteggi di secondo ordine la Proposizione T.4 diventa:
Equazioni caratteristiche del downcast di \mathrm{t} dal secondo ordine al primo, per tratteggi lineari
Sia T un tratteggio lineare di secondo ordine ed U un suo sottotratteggio di primo ordine. Sia t un trattino di entrambi, avente ordinale x in T ed y in U. Sia i l’indice della riga di t. Allora valgono le seguenti uguaglianze:
x = \begin{cases} y + \left \lfloor \frac{n_1 y - 1}{n_2} \right \rfloor & \text{se } i = 1\\ y + \left \lfloor \frac{n_2 y}{n_1} \right \rfloor & \text{se } i = 2 \end{cases} \tag{7}Equivalentemente, posto j tale che \{i, j\} = \{1, 2\}:
x = y + \left \lfloor \frac{n_i y - (j \gt i)}{n_j} \right \rfloor \tag{7$^{\prime}$}Vediamo ora cosa succede se T è di terzo ordine. In questo caso il sottotratteggio U può essere di primo o di secondo ordine.
Se U è di primo ordine, possiamo procedere in modo simile a prima, ottenendo il seguente Corollario:
Equazioni caratteristiche del downcast di \mathrm{t} dal terzo ordine al primo, per tratteggi lineari
Sia T un tratteggio lineare di terzo ordine ed U un suo sottotratteggio di primo ordine. Sia t un trattino di entrambi, avente ordinale x in T ed y in U. Sia i l’indice della riga di t. Allora valgono le seguenti uguaglianze:
x = \begin{cases} y + \left \lfloor \frac{n_1 y - 1}{n_2} \right \rfloor + \left \lfloor \frac{n_1 y - 1}{n_3} \right \rfloor & \text{se } i = 1\\ y + \left \lfloor \frac{n_2 y}{n_1} \right \rfloor + \left \lfloor \frac{n_2 y - 1}{n_3} \right \rfloor & \text{se } i = 2\\ y + \left \lfloor \frac{n_3 y}{n_1} \right \rfloor + \left \lfloor \frac{n_3 y}{n_2} \right \rfloor & \text{se } i = 3 \end{cases} \tag{8}Equivalentemente, posti j e k tali che \{i, j, k\} = \{1, 2, 3\}:
x = y + \left \lfloor \frac{n_i y - (j \gt i)}{n_j} \right \rfloor + \left \lfloor \frac{n_i y - (k \gt i)}{n_k} \right \rfloor \tag{8$^{\prime}$}Notiamo che la formula (8′) non è ambigua, sebbene la condizione \{i, j, k\} = \{1, 2, 3\} non definisca esattamente chi siano j e k. Infatti, se ad esempio i = 1, per avere \{i, j, k\} = \{1, 2, 3\}, potrebbe essere j = 2 e k = 3, oppure k = 2 e j = 3. Nel primo caso, sostituendo nella (8′), abbiamo:
x = y + \left \lfloor \frac{n_1 y - (2 \gt 1)}{n_2} \right \rfloor + \left \lfloor \frac{n_1 y - (3 \gt 1)}{n_3} \right \rfloorMentre nel secondo caso abbiamo:
x = y + \left \lfloor \frac{n_1 y - (3 \gt 1)}{n_3} \right \rfloor + \left \lfloor \frac{n_1 y - (2 \gt 1)}{n_2} \right \rfloorMa si tratta della stessa equazione, perché cambia solo l’ordine degli addendi. Ciò accade perché, nella (8′), l’espressione \left \lfloor \frac{n_i y - (j \gt i)}{n_j} \right \rfloor + \left \lfloor \frac{n_i y - (k \gt i)}{n_k} \right \rfloor è simmetrica rispetto a j e k, ossia non cambia se si scambiano i due simboli tra loro.
Il fatto che la (8′) sia simmetrica rispetto a j e k deriva direttamente dalla formula generale (6′), dalla quale è ricavata la (8′) supponendo che T sia di terzo ordine. L’espressione \left \lfloor \frac{n_i y - (j \gt i)}{n_j} \right \rfloor + \left \lfloor \frac{n_i y - (g \gt i)}{n_k} \right \rfloor presente nella (8′) è la scrittura espansa della seguente sommatoria presente nella (6′):
\sum_{i^{\prime} \neq i} \left \lfloor \frac{n_i y - (i \lt i^{\prime})}{n_{i^{\prime}}} \right \rfloor \tag{9}In pratica nella (8′) stiamo semplicemente chiamando j e k i due possibili valori dell’indice della sommatoria i^{\prime}, ossia i due indici diversi da i. Scambiare tra loro j e k significa quindi sommare gli addendi della sommatoria (9) in un ordine diverso, ma per la proprietà commutativa questo non cambia il risultato finale.
Osserviamo inoltre che nella formula (8), a differenza della (7), compaiono due parti intere e non una, perché questa volta stiamo scendendo di due ordini (dal terzo al primo) (v. osservazione precedente).
Supponiamo ora che il tratteggio U sia di secondo ordine, cioè U = T[i, j] per qualche j (i è fisso ed è sempre l’indice della riga del trattino t). In questo caso non possiamo partire dalle formule (6) e (6′), valide solo se U è di primo ordine, ma dobbiamo utilizzare le formule (4) e (4′). Consideriamo in particolare la formulazione compatta (4′).
Avendo posto U = T[i, j], esiste un solo indice i^{\prime} che non si riferisce ad una riga di U: possiamo chiamarlo k, con la solita condizione \{i, j, k\} = \{1, 2, 3\} (dove k questa volta è univocamente determinato: ad esempio, se (i, j) = (1, 2), allora k = 3). Quindi la sommatoria \sum_{i^{\prime}\ |\ T[i^{\prime}] \nsubseteq U} si riduce ad un solo elemento, con i^{\prime} = k, e la formula diventa:
Qui abbiamo nuovamente una sola parte intera, perché stiamo scendendo di un ordine solo, dal terzo al secondo.
A partire da questa formula, volendo, si possono ricavare le formule specifiche per ogni possibile scelta di i e j: le enunciamo nel seguente Corollario.
Equazioni caratteristiche del downcast di \mathrm{t} dal terzo ordine al secondo, per tratteggi lineari
Sia T) un tratteggio lineare di terzo ordine ed U = T[i, j] un suo sottotratteggio di secondo ordine. Sia t un trattino di entrambi, avente ordinale x in T ed y in U. Sia i l’indice della riga di t. Allora valgono le seguenti uguaglianze:
x = \begin{cases} y + \left \lfloor \frac{\mathrm{t\_valore}_U(y) - 1}{n_3} \right \rfloor & \text{se } (i, j) = (1, 2) \text{ oppure } (i, j) = (2, 1)\\ y + \left \lfloor \frac{\mathrm{t\_valore}_U(y) - 1}{n_2} \right \rfloor & \text{se } (i, j) = (1, 3) \\ y + \left \lfloor \frac{\mathrm{t\_valore}_U(y)}{n_2} \right \rfloor & \text{se } (i, j) = (3, 1) \\ y + \left \lfloor \frac{\mathrm{t\_valore}_U(y)}{n_3} \right \rfloor & \text{se } (i, j) = (2, 3) \text{ oppure } (i, j) = (3, 2) \end{cases} \tag{10}Equivalentemente, posto k tale che \{i, j, k\} = \{1, 2, 3\}:
x = y + \left \lfloor \frac{\mathrm{t\_valore}_U(y) - (k \gt i)}{n_k} \right \rfloor \tag{10$^{\prime}$}