Prerequisiti:
- Funzioni polinomiali e polinomi
- Definizione di limite di una successione e di una funzione
- Calcolo dei limiti in generale, calcolo del limite del rapporto tra due funzioni polinomiali
Buona parte dello studio della teoria dei numeri può essere condotto analizzando dei casi concreti, cioè partendo proprio dai conti numerici. Uno studio di questo tipo favorisce lo sviluppo di nuove idee e la comprensione di alcune tecniche dimostrative, tuttavia non si può prescindere dal verificare che quanto osservato sulla base degli esempi numerici valga in generale, per numeri arbitrariamente grandi. Alcune volte questa generalizzazione è immediata, altre volte sono richiesti gli strumenti di una parte dell’analisi matematica, detta analisi asintotica. Data l’importanza che riveste quest’argomento per i nostri scopi, ne richiamiamo alcuni elementi essenziali. Il livello di rigore matematico di questo articolo è sufficiente per i nostri scopi, ma non lo è in generale: per gli approfondimenti vi invitiamo a cercare nei vostri testi di analisi preferiti (nella nostra libreria trovate alcuni consigli).
L’esempio dei polinomi
Consideriamo le funzioni f(x) = 4 + x^2 e g(x) = x^3. Per i primi x interi non negativi, esse assumono i seguenti valori:
| x | f(x) | g(x) |
| 0 | 4 | 0 |
| 1 | 5 | 1 |
| 2 | 8 | 8 |
| 3 | 13 | 27 |
| 4 | 20 | 64 |
| 5 | 29 | 125 |
È evidente che le due funzioni tendono all’infinito, per x che tende all’infinito, e che la funzione g cresce più velocemente di f. Nonostante ciò, quest’ultima ha un “vantaggio iniziale” che le permette, per x = 0, 1, 2, di assumere valori superiori o uguali a quelli assunti dalla funzione g. In questo caso, guardando solo le prime tre righe della tabella, si potrebbe pensare che la funzione che assume valori più grandi sia f, mentre è sufficiente esaminare le altre tre righe per accorgersi che, in effetti, è vero il contrario.
Questa situazione è ancora più evidente se consideriamo valori di x più grandi e li mostriamo in un grafico. Vediamo così che il vantaggio iniziale della funzione f può essere considerato davvero insignificante:
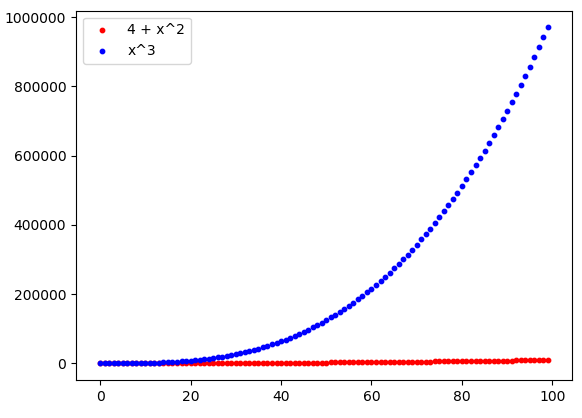
In questo contesto è di grande importanza l’analisi asintotica, perché consente di conoscere a priori, senza un esame numerico o grafico, quale di due funzioni assuma valori maggiori, per x che tende all’infinito. Questo però non basta. Un aspetto centrale di questa parte dell’analisi matematica è la definizione di ordini di infinito ed ordini di infinitesimo. Ad esempio, la funzione f definita prima è un infinito di ordine 2 perché è una funzione polinomiale di secondo grado, mentre la g è un infinito di ordine 3, essendo di terzo grado. Per questo motivo, secondo l’analisi asintotica, la funzione g cresce più velocemente di f e quindi, per x che tende all’infinito, g assumerà certamente, da un certo x in poi (per usare la terminologia dell’analisi, definitivamente), valori più grandi rispetto alla funzione f.
Consideriamo ora il caso di funzioni polinomiali dello stesso grado. Ad esempio, cosa ci dice l’analisi asintotica riguardo al confronto tra le funzioni h(x) = 20 + 2 x^2 e i(x) = 4 + 10 x^2? Per quanto visto prima, entrambe le funzioni hanno ordine di infinito 2. Ciò non toglie che una delle due possa essere definitivamente più grande dell’altra, come possiamo vedere nel seguente grafico:
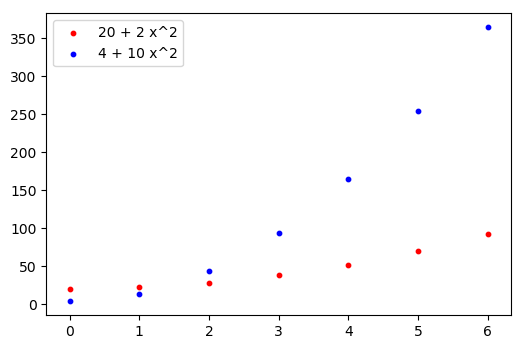
La funzione che ha il termine costante più grande, h, ha un piccolo vantaggio iniziale rispetto alla funzione i; ciononostante quest’ultima, al crescere di x, si rivela definitivamente più grande della prima, per la presenza di un coefficiente di x^2 più grande.
La situazione sembra simile a quella del confronto tra le funzioni f e g, ma vi è una differenza sostanziale: questa volta la maggiore crescita di una funzione rispetto all’altra non deriva da un maggiore esponente della x, ma da un coefficiente che non dipende da x, cioè la costante 10. Ciò significa che la situazione si capovolgerebbe moltiplicando una delle due funzioni per un’opportuna costante. Ad esempio, se moltiplicassimo la funzione i(x) per \frac{1}{10}, la funzione così ottenuta i'(x) = \frac{4}{10} + x^2 non è più asintoticamente maggiore di h(x), ma minore, avendo un coefficiente direttore minore (per “coefficiente direttore” si intende il coefficiente del termine di grado massimo).
La stessa cosa non può dirsi delle funzioni f(x) e g(x): per quante costanti possiamo provare, non ne troveremo mai una che, moltiplicata ad esempio per g, la renda definitivamente più piccola di f. Anche se, per esempio, moltiplicassimo g per \frac{1}{1.000}, ottenendo la funzione g'(x) = \frac{1}{1.000} x^3, questa funzione continuerebbe ad essere definitivamente più grande di f. Con un coefficiente costante piccolo abbiamo solo ritardato questo fenomeno, che si può osservare per valori più grandi di x; in ogni caso non è cambiato nulla nella prospettiva di studiare valori di x arbitrariamente grandi:
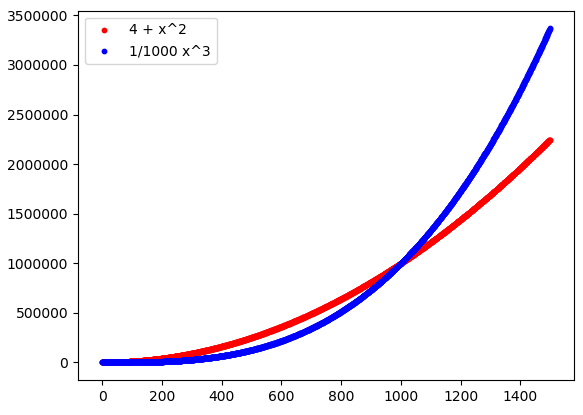
Riassumendo, nel confronto asintotico tra due funzioni possiamo distinguere due casi importanti, elencati nella seguente Definizione.
Relazioni asintotiche “o piccolo”, “theta”, “O grande”
Siano a e b due funzioni definite su un sottoinsieme di \mathbb{R} illimitato superiormente, a valori reali non negativi.
- Se la funzione a è definitivamente più piccola di b, e questo comportamento non cambia moltiplicando a o b per un’opportuna costante, si dice che a è un o piccolo di b, e si scrive a = o(b) oppure a \prec b o b \succ a.
- Se ciascuna delle due funzioni può essere resa definitivamente più piccola o più grande dell’altra, mediante la moltiplicazione per un’opportuna costante, si dice che a e b hanno lo stesso ordine, e si scrive a \asymp b o a = \Theta(b). Equivalentemente, dato che in questo caso le due funzioni hanno ruoli interscambiabili, si può scrivere anche b \asymp a o b = \Theta(a).
Inoltre, se si verifica uno dei due casi precedenti, si dice che la funzione a è un O grande di b, e si scrive a = O(b) oppure a \ll b oppure b \gg a. Quindi
Nel complesso, le relazioni funzionali del tipo a = o(b), a \asymp b e a = O(b) (con le sue equivalenti) prendono il nome di relazioni asintotiche.
Nella formulazione della Definizione A.1, è stato precisato che le due funzioni devono essere definite su un sottoinsieme di \mathbb{R} illimitato superiormente. Questo è necessario per poter studiare il comportamento delle funzioni andando all’infinito.
Nel caso delle funzioni polinomiali, i casi previsti dalla Definizione A.1 si possono esprimere come indicato nella seguente tabella:
| Relazione asintotica generale | Caso di funzioni polinomiali | Esempio |
|---|---|---|
| a = o(b) | a ha grado più basso di b | a(x) = f(x) = 4 + x^2, b(x) = g(x) = x^3 |
| a \asymp b | a e b hanno lo stesso grado | a(x) = h(x) = 20 + 2 x^2, b(x) = i(x) = 4 + 10 x^2 |
| a = O(b) | a ha grado minore o uguale a quello di b | Entrambi gli esempi precedenti |
Analizziamo ora un caso particolare.
Abbiamo visto che, se due funzioni polinomiali a(x) e b(x) hanno lo stesso grado, allora quella asintoticamente più grande è quella avente il coefficiente direttore più grande. E se il coefficiente direttore fosse lo stesso? Cosa si può dire ad esempio riguardo alle funzioni a(x) = 1 + x + 2 x^2 e b(x) = 2 + 3x + 2 x^2? Essendo uguale il termine di grado massimo 2 x^2, che è quello che “pesa” di più andando all’infinito, queste funzioni sono talmente simili in senso asintotico, che possono essere considerate equivalenti. Si introduce quindi la seguente definizione:
Equivalenza asintotica, caso di funzioni polinomiali
Se due funzioni polinomiali a e b hanno lo stesso grado e lo stesso coefficiente direttore, si scrive
e si legge “a è asintoticamente equivalente a b“.
Due definizioni più generali
Finora abbiamo parlato dell’analisi asintotica prendendo come riferimento il caso dei polinomi, che è sufficiente per capire i meccanismi di fondo. Abbiamo formulato la Definizione A.1, nella cui formulazione tuttavia non rientrano i polinomi: in effetti questa definizione può essere utilizzata per generiche funzioni, diversamente dalla Definizione A.2, che vale solo per i polinomi. Ora portiamo un passo avanti la generalizzazione che è cominciata con la Definizione A.1, in modo da ottenere una nuova definizione che:
- Comprenda sia la Definizione A.1 che la Definizione A.2;
- Valga anche per funzioni a valori negativi
- Sia scritta in modo da essere facilmente utilizzabile nei calcoli.
Possiamo raggiungere questi scopi sia col concetto di limite che senza. Vediamo prima la formulazione senza limiti e poi, chi vorrà, potrà vedere anche l’altra.
Relazioni asintotiche, definizioni alternative utilizzando le disuguaglianze
Siano a e b due funzioni definite su un sottoinsieme di \mathbb{R} illimitato superiormente, a valori reali. Sia la funzione b definitivamente positiva.
Se esiste una costante reale positiva A per cui definitivamente
allora a si dice O grande di b e si scrive a = O(b) oppure a \ll b oppure b \gg a. In particolare:
- Se la relazione (1) vale definitivamente per ogni costante reale positiva A, allora a si dice o piccolo di b, e si scrive a = o(b)
- Se esiste anche una costante reale positiva B per cui la (1) può essere estesa a sinistra con la disuguaglianza B b(x) \leq |a(x)|, cioè se esistono due costanti reali positive A e B tali che definitivamente
B b(x) \leq |a(x)| \leq A b(x) \tag{2}
allora a si dice dello stesso ordine di b e si scrive a \asymp b oppure a = \Theta(b). In questo caso i ruoli di a e b possono essere scambiati, per cui anche b \asymp a.
- Se la (2) senza il valore assoluto
B b(x) \leq a(x) \leq A b(x) \tag{2'}
vale definitivamente per ogni A \gt 1 e per ogni B \lt 1, allora a si dice asintoticamente equivalente a b e si scrive a \sim b. In tal caso, come prima, anche b \sim a.
Come abbiamo visto, a = O(b) si può scrivere anche come a \ll b oppure come b \gg a. La prima notazione è la più comune ma a volte, specie nei contesti più avanzati, i simboli \ll e \gg sono preferibili per due motivi:
- Evitano di inserire parentesi all’interno delle espressioni. Questo facilita la lettura delle formule, soprattutto quando la funzione che dovrebbe stare dentro la O grande (la b della definizione) è data da un’espressione molto lunga.
- Sono intuitivi, perché ricordano i simboli di minore e maggiore che compaiono dentro la definizione di O grande. Ad esempio, a \ll b e a = O(b) significano entrambe che esiste una costante positiva A tale che definitivamente |a(x)| \leq A b(x), ma con la prima notazione quest’aspetto è più evidente. Se volete, potete leggere i simboli \ll e \gg rispettivamente come “definitivamente minore di, a meno di un fattore costante” e “definitivamente maggiore di, a meno di un fattore costante”: queste espressioni rendono l’idea, nascondendo alcuni dettagli spesso inutili (il valore assoluto, che non serve per funzioni sempre positive, e la possibile uguaglianza, che può essere eliminata semplicemente aumentando la costante) e altri dettagli dati per scontato (la positività della costante).
Rivediamo gli esempi con cui abbiamo introdotto l’argomento, alla luce della Definizione A.3:
- Considerando le funzioni polinomiali f(x) = 4 + x^2 e g(x) = x^3, si ha che f = O(g), perché possiamo trovare una costante reale positiva A tale che definitivamente |f(x)| = f(x) \leq A g(x), ossia 4 + x^2 \leq A x^3. Questa costante può essere semplicemente 1: infatti, come abbiamo visto nella Figura 1, definitivamente 4 + x^2 \leq x^3.
- In particolare, f = o(g), perché nel punto precedente potevamo scegliere, in realtà, qualsiasi costante. Infatti, come abbiamo visto nella Figura 3, anche scegliendo una costante A molto piccola, definitivamente si ha sempre che 4 + x^2 \leq A x^3 (questo, naturalmente, dovrebbe essere dimostrato in maniera formale. Se ci volete provare, ponete 4 + x^2 \leq A x^3: facendo i conti, troverete una x a partire dalla quale la disuguaglianza è verificata: in altre parole, la disuguaglianza è valida definitivamente, che è esattamente ciò che è richiesto).
- Considerando le funzioni polinomiali h(x) = 20 + 2 x^2 ed i(x) = 4 + 10 x^2, si ha che h = \Theta(i). Infatti possiamo trovare delle costanti reali positive A e B tali che definitivamente B i(x) \leq h(x) \leq A i(x), ossia B (4 + 10 x^2) \leq 20 + 2 x^2 \leq A (4 + 10 x^2), ad esempio A = 5 e B = \frac{1}{5}:
\begin{aligned}\frac{1}{5} (4 + 10 x^2) \leq 20 + 2 x^2 \leq 5 (4 + 10 x^2) \iff\\ \frac{4}{5} + 2 x^2 \leq 20 + 2 x^2 \leq 20 + 50 x^2 \end{aligned}
Questa disuguaglianza vale sempre e quindi, a maggior ragione, vale definitivamente.
- Considerando le funzioni a(x) = 1 + x + 2x^2 e b(x) = 2 + 3x + 2x^2, per verificare che a \sim b dobbiamo vedere se la disuguaglianza
B (2 + 3x + 2x^2) \leq 1 + x + 2x^2 \leq A (2 + 3x + 2x^2) \tag{3}
vale definitivamente per ogni A \gt 1 e per ogni B \lt 1:
- Per quanto riguarda la costante A, la cosa è abbastanza evidente in quanto 1 + x + 2x^2 \leq 2 + 3x + 2x^2 per x \geq 0. Quindi la seconda parte della (3) vale definitivamente per A = 1 e quindi a maggior ragione per A \gt 1;
- Per quanto riguarda B, possiamo riscrivere la prima parte della disuguaglianza come
(2B - 1) + (3B - 1)x \leq 2(1 - B) x^2 \tag{4}
Dobbiamo dimostrare che questa disuguaglianza vale definitivamente se B \lt 1. In questo caso il coefficiente di x^2, 2 (1 - B), è positivo, quindi lo è tutto il termine a destra. Abbiamo quindi due polinomi: uno a destra, di secondo grado e sempre positivo, 2(1 - B) x^2, ed uno a sinistra, di cui non conosciamo il segno ma sappiamo che è di primo grado, (2B - 1) + (3B - 1)x. Essendo di grado inferiore, il polinomio a sinistra è un “o piccolo” dell’altro, quindi la disuguaglianza (2B - 1) + (3B - 1)x \leq A 2(1 - B) x^2 vale definitivamente per ogni A: in particolare vale definitivamente per A = 1, che è appunto la (4).
Segue la definizione equivalente che usa il concetto di limite, per chi ha familiarità con esso.
Relazioni asintotiche, definizioni alternative utilizzando i limiti
Siano a e b due funzioni definite su un sottoinsieme di \mathbb{R} illimitato superiormente, a valori reali. Supponiamo per semplicità che a(x) sia sempre diverso da zero. Sia
Se L esiste ed è un numero reale, a si dice O grande di b e si scrive a = O(b). In particolare:
- Se L = 0, a si dice o piccolo di b e si scrive a = o(b).
- Se L = 1, a si dice asintoticamente equivalente a b e si scrive a \sim b. In questo caso i ruoli di a e b possono essere scambiati, per cui anche b \sim a.
- Se L \neq 0, compreso il caso precedente, a si dice dello stesso ordine di b e si scrive a \asymp b o a = \Theta(b). Anche in questo caso, come prima, si ha che anche b \asymp a.
Il caso delle funzioni asintoticamente equivalenti è particolarmente interessante. Per la Definizione A.4, in questo caso
Se vale questo, significa che le funzioni a e b sono completamente interscambiabili nel calcolo dei limiti. Ciò è particolarmente importante dal punto di vista analitico: ad esempio in questo modo si può calcolare un limite che coinvolge funzioni “difficili” sostituendole con funzioni equivalenti ma più “facili”.
La Definizione A.4 è, tra le definizioni formali delle relazioni asintotiche, quella più “pulita” e concisa; tuttavia ha il difetto di essere applicabile solo in espressioni algebriche dove sono stati esplicitamente introdotti i limiti. Negli altri casi è bene tenere a mente anche la Definizione A.3.
Per maggiore chiarezza, e per riferimento futuro, riassumiamo le Definizioni A.1, A.3 ed A.4, assieme al caso delle funzioni polinomiali, nella seguente tabella riassuntiva. I più volenterosi potranno esercitarsi a dimostrare l’equivalenza tra le tre definizioni; tuttavia per i nostri scopi è sufficiente ricordarle, sapendo che sono equivalenti, e saperle applicare, come faremo nel seguito.
| Relazione asintotica (notazioni alternative) | Relazione equivalente | Definizione A.1 | Definizione A.3 | Definizione A.4 | Caso di funzioni polinomiali |
|---|---|---|---|---|---|
| a = O(b) | a = o(b) \textrm{ oppure } a \asymp b | Esiste una costante reale positiva A per cui definitivamente |a(x)| \leq A b(x) | Il limite \lim_{x \to +\infty} \frac{a(x)}{b(x)} esiste ed è un numero reale | a ha grado minore o uguale a quello di b | |
| a = o(b) (a \prec b, b \succ a) | La funzione a è definitivamente più piccola di b, e questo comportamento non cambia moltiplicando a o b per una costante | Per ogni costante reale positiva A, definitivamente |a(x)| \leq A b(x) | \lim_{x \to +\infty} \frac{a(x)}{b(x)} = 0 | a ha grado più basso di b | |
| a \asymp b (a = \Theta(b)) | b \asymp a (b = \Theta(a)) | Ciascuna delle due funzioni può essere resa definitivamente più piccola o più grande dell’altra, mediante la moltiplicazione per un opportuno termine costante | Esistono due costanti reali positive A e B tali che definitivamente B b(x) \leq |a(x)| \leq A b(x) | \lim_{x \to +\infty} \frac{a(x)}{b(x)} \neq 0 ed è un numero reale | a e b hanno lo stesso grado |
| a \sim b | b \sim a | per ogni costante reale A \gt 1 ed ogni costante reale B \lt 1, B b(x) \leq a(x) \leq A b(x) | \lim_{x \to +\infty} \frac{a(x)}{b(x)} = 1 | a e b hanno lo stesso grado e lo stesso coefficiente direttore |
Nella teoria dei numeri utilizzeremo l’analisi asintotica in un contesto molto particolare, ossia per x che tende all’infinito e per valori interi di x.